Shmidt group
A finite non-nilpotent group all proper subgroups of which are nilpotent (cf. Nilpotent group). A Shmidt group is a solvable group of order 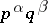 , where
, where 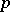 and
and 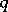 are different prime numbers. In any finite non-nilpotent group there are subgroups that are Shmidt groups. They were introduced by O.Yu. Shmidt in 1924.
are different prime numbers. In any finite non-nilpotent group there are subgroups that are Shmidt groups. They were introduced by O.Yu. Shmidt in 1924.
References
| [1] | O.Yu. Shmidt, , Selected works on mathematics , Moscow (1959) pp. 221–227 (In Russian) |
Comments
Shmidt's problem (also spelled Smidt's problem) asks which infinite groups are such that every proper subgroup is finite. These groups are sometimes also called Shmidt groups (in the Russian literature). The answer is as follows. Let 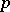 be a prime number. There is a unique imbedding of cyclic groups
be a prime number. There is a unique imbedding of cyclic groups
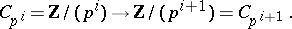 |
The direct limit is the quasi-cyclic group
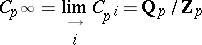 |
(where 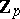 is the ring of integers of the
is the ring of integers of the 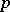 -adic completion
-adic completion 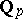 of the rational numbers). A group is locally finite if every finite subset generates a finite subgroup. One now has the result that if an infinite locally finite group has only finite subgroups, then it is one of the quasi-cyclic groups
of the rational numbers). A group is locally finite if every finite subset generates a finite subgroup. One now has the result that if an infinite locally finite group has only finite subgroups, then it is one of the quasi-cyclic groups 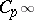 . Such a group is also called a Prüfer group.
. Such a group is also called a Prüfer group.
References
| [a1] | B.A.F. Wehrfritz, "Locally finite groups" , North-Holland (1973) pp. Chapt. 2, Thm. 2.6 |
| [a2] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) pp. Chapt. 1, §2 (Translated from Russian) |
Shmidt group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shmidt_group&oldid=48687