Sheppard corrections

for moments

Corrections to the discretization of the realizations of continuous random variables, used in order to diminish systematic errors in the problem of estimating the moments of the continuous random variables under a given system of rounding-off. Such corrections were first proposed by W.F. Sheppard [1].

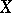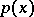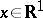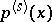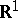Let be a continuously-distributed random variable for which the probability density , , has an everywhere continuous derivative of order on such that

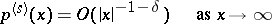for some 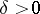, and let the moments (cf. Moment) exist. Further, let a system of rounding-off the results of observations be given (i.e. an origin 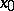and a step 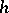, , 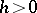are given), the choice of which leads to the situation, when instead of the realizations of the initial continuous random variable 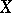, in reality one observes realizations 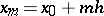, 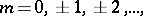of a discrete random variable

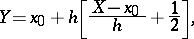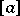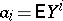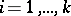where is the integer part of . The moments , , of 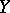are computed from the formula

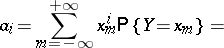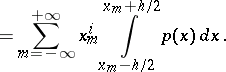Generally speaking, 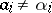. Thus a question arises: Is it possible to adjust the moments in order to obtain "good" approximations to the moments ? The Sheppard corrections give a positive answer to this question.

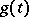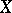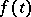Let be the characteristic function of the random variable , let be the characteristic function of the random variable 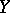, and let

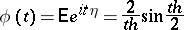be the characteristic function of a random variable 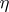which is uniformly distributed on 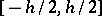and which is stochastically independent of 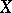. Under these conditions, for a small ,

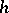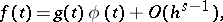hence the moments of the discrete random variable 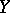coincide up to 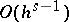with the moments of the random variable 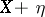and, thus, up to 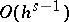, the following equalities hold:

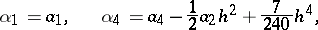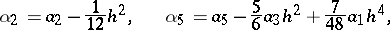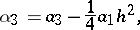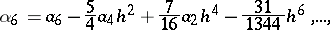which contain the so-called Sheppard corrections for the moments .

References

[1]	W.F. Sheppard, "On the calculation of the most probable values of frequency-constants, for data arranged according to equidistant divisions of a scale" Proc. Lond. Math. Soc. , 29 (1898) pp. 353–380
[2]	H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946)
[3]	S.S. Wilks, "Mathematical statistics" , Wiley (1962)
[4]	B.L. van der Waerden, "Mathematische Statistik" , Springer (1957)