Sharp form

An -dimensional differential form on an open subset such that the co-mass (cf. Mass and co-mass) and the co-mass Lipschitz constant

where and is the length of the vector , are finite. The number

is known as the sharp norm of the form .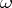

Whitney's theorem. To each -dimensional sharp cochain in corresponds a unique -dimensional sharp form for which

for all -dimensional oriented simplices ; 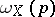is defined by the formula

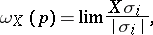where is a sequence of simplices containing the point , with diameters tending to zero, and lying in the same plane. This correspondence is a one-to-one mapping of the space of cochains into the space of sharp forms; moreover:

, i.e. the co-mass of ;

, i.e. the Lipschitz constant of ;

, i.e. the sharp norm of ;

is a Banach space.

In particular, there is a correspondence between zero-dimensional sharp cochains and sharp functions (bounded functions which satisfy a Lipschitz condition).

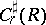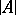The space of -dimensional sharp chains of finite mass with the sharp norm 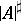is isomorphic to the space of additive set functions whose values are -vectors , provided with the sharp norm 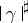; this correspondence is defined by the formula:

(*)

for any cochain 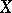, where is the -dimensional sharp form corresponding to the cochain , and

, i.e. the covector of the chain ;

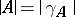, i.e. the complete variation of ;

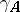, i.e. the sharp norm of the chain .

Thus, (*) is a generalization of the ordinary Lebesgue–Stieltjes integral. In particular, the Lebesgue-measurable summable function 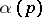associated with (cf. Flat form), i.e.

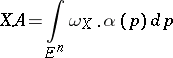for any cochain , exists for 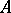if and only if 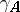is absolutely continuous.

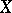If is a regular form and is a sharp cochain, then there exists a form , and Stokes' formula

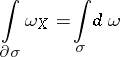applies. Other results established for regular forms can be generalized in an analogous manner.

For references see Sharp norm.