Semi-hyperbolic space
A projective  -space in which the metric is defined by a given absolute consisting of the following collection: a second-order real cone
-space in which the metric is defined by a given absolute consisting of the following collection: a second-order real cone 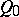 of index
of index 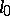 with an
with an 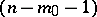 -plane vertex
-plane vertex 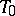 ; a real
; a real 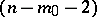 -cone
-cone 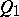 of index
of index 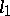 with an
with an 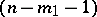 -plane vertex
-plane vertex 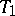 in the
in the 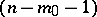 -plane
-plane 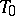 ;
;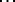 ; a real
; a real 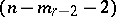 -cone
-cone 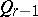 of index
of index 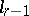 with an
with an 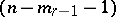 -plane vertex
-plane vertex 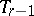 ; and a non-degenerate real
; and a non-degenerate real 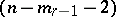 -quadric
-quadric 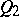 of index
of index 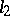 in the plane
in the plane 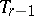 ;
; 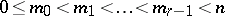 . This is the definition of a semi-hyperbolic space with indices
. This is the definition of a semi-hyperbolic space with indices 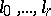 ; it is denoted by
; it is denoted by 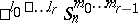 .
.
If the cone 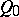 is a pair of merging planes, both identical with
is a pair of merging planes, both identical with 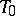 (for
(for 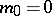 ), the semi-hyperbolic plane with the improper plane
), the semi-hyperbolic plane with the improper plane 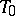 is called a semi-Euclidean space:
is called a semi-Euclidean space:
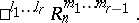 |
The distance between two points 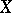 and
and 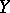 is defined as a function of the position of the straight line
is defined as a function of the position of the straight line 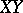 relative to the planes
relative to the planes 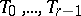 . In particular, if
. In particular, if 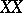 does not intersect
does not intersect 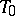 , the distance between
, the distance between 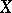 and
and 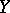 is defined through a scalar product, in analogy with the appropriate definition in a quasi-hyperbolic space. If
is defined through a scalar product, in analogy with the appropriate definition in a quasi-hyperbolic space. If 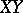 intersects
intersects 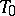 but does not intersect
but does not intersect 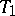 , or it intersects
, or it intersects 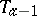 but does not intersect
but does not intersect 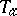 , the distance between the points is defined as the scalar product with itself of the distance between the vectors of the points
, the distance between the points is defined as the scalar product with itself of the distance between the vectors of the points 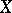 and
and 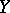 .
.
Depending on the position of the absolute relative to the planes 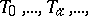 one distinguishes four types of straight lines of different orders: elliptic, hyperbolic, isotropic, and parabolic.
one distinguishes four types of straight lines of different orders: elliptic, hyperbolic, isotropic, and parabolic.
The angles between the planes in a semi-hyperbolic space are defined analogous to the angles between the planes in a quasi-hyperbolic space, i.e. using distance in the dual space.
A projective metric in a semi-hyperbolic space is a metric of the most general form. A particular case of such a metric is a metric of a quasi-hyperbolic space. In particular, the  -plane
-plane 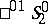 is identical with the pseudo-Euclidean space
is identical with the pseudo-Euclidean space 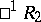 , the plane
, the plane 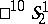 — with the co-pseudo-Euclidean space
— with the co-pseudo-Euclidean space 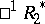 ; the
; the  -spaces
-spaces 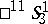 and
and 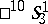 coincide with the quasi-hyperbolic
coincide with the quasi-hyperbolic  -space, the
-space, the  -space
-space 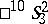 — with the co-pseudo-Euclidean space
— with the co-pseudo-Euclidean space 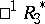 , etc. The
, etc. The  -space
-space 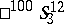 is dual to the pseudo-Galilean space
is dual to the pseudo-Galilean space 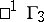 , it is known as a co-pseudo-Galilean space; its absolute consists of pairs of real planes (a cone
, it is known as a co-pseudo-Galilean space; its absolute consists of pairs of real planes (a cone 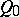 ) and a point
) and a point 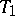 on the straight line
on the straight line 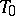 in which these planes intersect.
in which these planes intersect.
The motions of a semi-hyperbolic space are defined as collineations of the space which map the absolute into itself. If 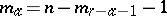 and
and 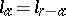 , a semi-hyperbolic space is dual to itself. It is then possible to define co-motions, the definition being analogous to that of co-motions in a self-dual quasi-hyperbolic space. The group of motions and the group of motions and co-motions are Lie groups. The motions (and co-motions) of a semi-hyperbolic space are described by pseudo-orthogonal operators with indices determined by the indices of the space.
, a semi-hyperbolic space is dual to itself. It is then possible to define co-motions, the definition being analogous to that of co-motions in a self-dual quasi-hyperbolic space. The group of motions and the group of motions and co-motions are Lie groups. The motions (and co-motions) of a semi-hyperbolic space are described by pseudo-orthogonal operators with indices determined by the indices of the space.
A semi-hyperbolic space is a semi-Riemannian space.
References
| [1] | D.M.Y. Sommerville, Proc. Edinburgh Math. Soc. , 28 (1910) pp. 25–41 |
| [2] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
Comments
References
| [a1] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
Semi-hyperbolic space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-hyperbolic_space&oldid=48661