Semi-continuous summation method

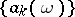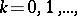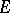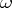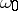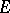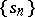A summation method (cf. Summation methods) for series and sequences, defined by means of sequences of functions. Let , be a sequence of functions defined on some set of variation of the parameter , and let be an accumulation point of (finite or infinite). The functions are used to convert a given sequence into a function :

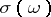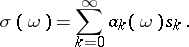(1)

If the series in (1) is convergent for all sufficiently close to 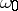, and if

one says that the sequence is summable to by the semi-continuous summation method defined by the sequence 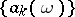. If 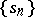is the sequence of partial sums of the series

(2)

one says that the series (2) is summable by the semi-continuous method to . A semi-continuous summation method with 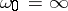is an analogue of the matrix summation method defined by the matrix 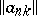, in which the integer-valued parameter is replaced by the continuous parameter 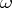. The sequence of functions 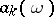is therefore known as a semi-continuous matrix.

A semi-continuous summation method can be defined by direct transformation of a series into a function, using a given sequence of functions, say :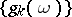

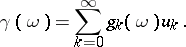(3)

In this case the series (2) is said to be summable to if

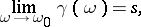where 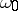is an accumulation point of the set 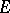of variation of 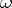, and the series (3) is assumed to be convergent for all 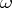sufficiently close to .

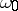In some cases a semi-continuous summation method is more convenient than a summation method based on ordinary matrices, since it enables one to utilize tools of function theory. Examples of semi-continuous summation methods are: the Abel summation method, the Borel summation method, the Lindelöf summation method, and the Mittag-Leffler summation method. The class of semi-continuous methods also includes methods with semi-continuous matrices of the form

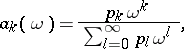where the denominator is an entire function that does not reduce to a polynomial.

Conditions for the regularity of semi-continuous summation methods are analogous to regularity conditions for matrix summation methods. For example, the conditions

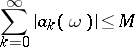for all 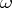sufficiently close to ,

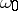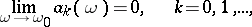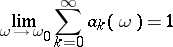are necessary and sufficient for the semi-continuous summation method defined by the transformation (1) of 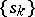into a function to be regular (see Regularity criteria).

References

[1]	G.H. Hardy, "Divergent series" , Clarendon Press (1949)
[2]	R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950)
[3]	W. Beekmann, K. Zeller, "Theorie der Limitierungsverfahren" , Springer (1970)