Semi-Riemannian space

A space with a semi-Riemannian metric (with a degenerate metric tensor). A semi-Riemannian space is a generalization of the concept of a Riemannian space. The definition of a semi-Riemannian space can be expressed in terms of the concepts used in the definition of a Riemannian space. In the definition of a Riemannian space 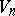one uses as tangent space the space 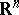with a Euclidean metric, which is supposed to be invariant under parallel displacements of 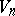(the metric tensor 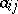of the space 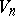is absolutely constant). If the tangent space at every point of 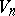is equipped with the structure of a semi-Euclidean space 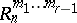, then the metric of the space 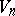is degenerate, the metric tensor is also absolutely constant but is now degenerate, its matrix has rank 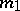and has a non-singular submatrix. One defines a second degenerate metric tensor in the 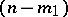-plane 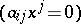, which is called the zero 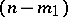-plane of the tensor 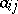; its matrix also possesses a non-singular submatrix, etc. 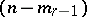The last, -th metric tensor, defined in the zero -plane of the 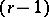-st tensor, is a non-degenerate tensor with a non-singular matrix. Such a space is called a semi-Riemannian space, and in this case it is denoted by the symbol 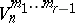. Analogously one defines semi-Riemannian spaces of the form 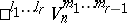, that is, when the tangent space has the structure of a semi-pseudo-Euclidean space 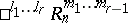. The spaces 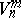and 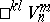are called quasi-Riemannian spaces.

As in a Riemannian space, one introduces the concept of curvature in a -dimensional direction. Semi-hyperbolic and semi-elliptic spaces are semi-Riemannian spaces of constant non-zero curvature, and a semi-Euclidean space is a semi-Riemannian space of constant curvature zero.

Thus, a semi-Riemannian space can be defined as a space of affine connection (without torsion) whose tangent spaces at every point are semi-Euclidean (or semi-pseudo-Euclidean), and where the metric tensor of the semi-Riemannian space is absolutely constant.

In a semi-Riemannian space, the differential geometry of lines and surfaces is constructed by analogy with the differential geometry of lines and surfaces in 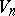, taking into account the special features of semi-Riemannian spaces indicated above. Surfaces of semi-hyperbolic and semi-elliptic spaces are themselves semi-Riemannian spaces. In particular, the 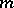-horosphere 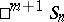in a semi-hyperbolic space is isometric to the semi-Riemannian space 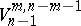, the metric of which can be reduced to the metric of the semi-elliptic space 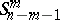; this fact is a generalization of the isometry of a horosphere in Lobachevskii space to a Euclidean space.

References

[1]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)

References

[a1]	B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian)
[a2]	B. O'Neill, "Semi-Riemannian geometry (with applications to relativity)" , Acad. Press (1983)