Second dual space

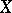The space dual to the space , where is the strong dual to a Hausdorff locally convex space , i.e. is equipped with the strong topology. Each element generates an element in accordance with the formula (). If , the space is semi-reflexive. If is a barrelled space, the linear mapping defined by is an isomorphic imbedding of the space 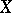into the space . The imbedding is called canonical. For normed spaces 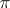is an isometric imbedding.

Comments

The second dual is also called the bidual.

For (semi-) reflexivity see also Reflexive space. For the (first) dual space see Adjoint space. The space 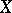is reflexive if the canonical imbedding is surjective and also the two topologies coincide, where is given the strong topology defined by the dual pair . For Banach spaces semi-reflexivity is the same as reflexivity.

References

[a1]	D. van Dulst, "Reflexive and superreflexive spaces" , MC Tracts , 102 , Math. Centre (1978)
[a2]	G. Köthe, "Topological vector spaces" , 1 , Springer (1969) pp. §23.5