Schwarz lemma
Let  be a holomorphic function on the disc
be a holomorphic function on the disc  , with
, with  and
and  in
in  ; then
; then
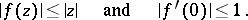 | (1) |
If equality holds for a single  , then
, then  , where
, where  is a real constant (the classical form of the Schwarz lemma). This lemma was proved by H.A. Schwarz (see [1]).
is a real constant (the classical form of the Schwarz lemma). This lemma was proved by H.A. Schwarz (see [1]).
Various versions of the Schwarz lemma are known. For instance, the following invariant form of the Schwarz lemma: If a function 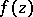 is holomorphic in the disc
is holomorphic in the disc 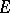 and if
and if  in
in  , then for any points
, then for any points 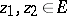 ,
,
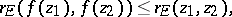 | (2) |
where  is the hyperbolic distance between two points
is the hyperbolic distance between two points  in
in 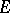 (see Hyperbolic metric); further, for
(see Hyperbolic metric); further, for 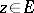 one has
one has
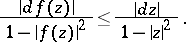 | (3) |
Equality holds in (2) and (3) only if 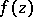 is a biholomorphic mapping of
is a biholomorphic mapping of  onto itself.
onto itself.
Inequality (3) is also called the differential form of the Schwarz lemma. Integrating this inequality leads to the following formulation of the Schwarz lemma: If the disc 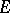 is transformed by a holomorphic function
is transformed by a holomorphic function 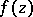 such that
such that 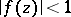 for
for 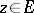 , then the hyperbolic length of an arbitrary arc in
, then the hyperbolic length of an arbitrary arc in 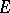 decreases, except in the case when
decreases, except in the case when 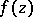 is a univalent conformal mapping of
is a univalent conformal mapping of 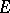 onto itself; in this case hyperbolic distances between points are preserved.
onto itself; in this case hyperbolic distances between points are preserved.
The principle of the hyperbolic metric (cf. Hyperbolic metric, principle of the) is a generalization of the invariant form of the Schwarz lemma to multiply-connected domains on which a hyperbolic metric can be defined. Analogues of the Schwarz lemma for holomorphic mappings in the  -dimensional complex space
-dimensional complex space 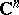 are known (see [4]).
are known (see [4]).
References
| [1] | H.A. Schwarz, "Gesamm. math. Abhandl." , 1–2 , Springer (1890) |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [3] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [4] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
Comments
Schwarz ([1]) stated this result for univalent functions only. The formulation, designation and systematic use of this lemma in the general form stated above is due to C. Carathéodory [a2]. For the history of this result, see [a3], pp. 191-192.
The inequalities (2) and (3) are also known as the Schwarz–Pick lemma. Equality (2) can be written in the equivalent form
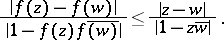 |
For an extensive treatment of the Schwarz lemma and its many generalizations and applications see [a1].
References
| [a1] | S. Dineen, "The Schwarz lemma" , Oxford Univ. Press (1989) |
| [a2] | C. Carathéodory, "Untersuchungen über die konformen Abbildungen von festen und veränderlichen Gebieten" Math. Ann. , 72 (1912) pp. 107–144 |
| [a3] | R.B. Burchel, "An introduction to classical complex analysis" , 1 , Birkhäuser (1979) |
| [a4] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) pp. 381, Thm. 17.8 (Translated from Russian) |
| [a5] | L.V. Ahlfors, "Conformal invariants. Topics in geometric function theory" , McGraw-Hill (1973) |
| [a6] | J.-B. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [a7] | W. Rudin, "Function theory in the unit ball in  " , Springer (1980) " , Springer (1980) |
Schwarz lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schwarz_lemma&oldid=48634