Schottky theorem

If a function

(*)

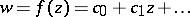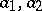is regular and analytic in the disc and does not take certain finite values in , then in any disc , , the modulus is bounded by a number 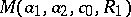that depends only on 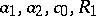(see [1]). A more complete formulation can be obtained, by combining the generalized Schottky theorem and Landau's theorem, for an arbitrary number 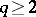of exceptional values. Suppose that the function (*) does not take some finite values 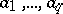, 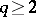. Then for 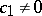, the radius 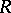is bounded above by a number that depends only on 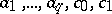(Landau's theorem). Moreover, in the disc , , the modulus 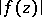is bounded by a number 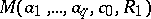that depends only on 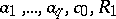(Schottky's theorem).

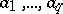From the geometrical point of view Schottky's theorem means that the spherical distance (i.e. the distance on the Riemann sphere) of the image of the disc from the points is no less than a number 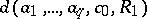that depends only on 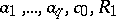. Schottky's theorem is one of the classical results in the theory of functions of a complex variable of the type of distortion theorems.

References

[1]	F. Schottky, "Ueber den Picard'schen Satz und die Borel'schen Ungleichungen" Sitzungsber. Preuss. Akad. Wiss. , 2 (1904) pp. 1244–1262
[2]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[3]	S. Stoilov, "The theory of functions of a complex variable" , 1–2 , Moscow (1962) (In Russian; translated from Rumanian)

Comments

The theorems of Landau and Schottky are also related to the Picard theorem.

References

[a1]	E. Landau, D. Gaier, "Darstellung und Begrundung einiger neuerer Ergebnisse der Funktionentheorie" , Springer, reprint (1986)
[a2]	J.B. Conway, "Functions of one complex variable" , Springer (1978)