Saxon-Hutner theorem
A theorem concerning energy gaps in one-dimensional random alloy models described by the Schrödinger equation or the Dirac equation. It states that forbidden energies that are common to a pure crystal  and a pure crystal
and a pure crystal 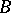 (with the same lattice constant) will always be forbidden energies in any arrangement of the atoms of
(with the same lattice constant) will always be forbidden energies in any arrangement of the atoms of 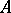 and
and 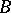 in a substitutional solid solution.
in a substitutional solid solution.
Making use of the one-to-one correspondence between the real localized atomic potentials and 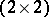 -transfer matrices belonging to any of the isomorphic three-dimensional Lie groups
-transfer matrices belonging to any of the isomorphic three-dimensional Lie groups 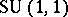 ,
, 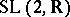 or
or 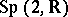 , this can be described in mathematical terms as follows. If
, this can be described in mathematical terms as follows. If 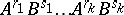 is an arbitrary linear chain consisting of two types of atoms
is an arbitrary linear chain consisting of two types of atoms 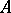 and
and 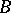 , each having representatives
, each having representatives 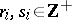 in the
in the 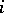 th period. Then the group nature of the individual transfer matrices
th period. Then the group nature of the individual transfer matrices 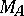 and
and 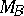 makes it possible to express the total transfer matrix
makes it possible to express the total transfer matrix 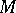 of the elementary cell as the product
of the elementary cell as the product  , and the forbidden energies for electrons propagating there are given by the condition
, and the forbidden energies for electrons propagating there are given by the condition 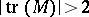 .
.
In the transfer-matrix approach, the theorem takes the form of the following question: Given that
 |
is it true that for any arrangement 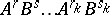 of atoms of type
of atoms of type 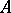 and
and 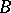 one has
one has
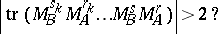 |
Relying on quite different techniques, several non-equivalent sufficient conditions guaranteeing its validity have been derived.
References
| [a1] | D. Saxon, R. Hutner, Philips Res. Rep. , 4 (1949) pp. 81 |
| [a2] | H. Matsuda, Progr. Theor. Phys. , 27 (1962) pp. 81 |
| [a3] | J. Hori, Progr. Theor. Phys. , 32 (1964) pp. 371 |
| [a4] | L. Dworin, Phys. Rev. , 138 A (1965) pp. 1121 |
| [a5] | B. Tong, S. Tong, Phys. Rev. , 180 (1969) pp. 739 |
| [a6] | I. Mladenov, C.R. Acad. Sci. (Sofia) , 38 (1985) pp. 993 |
| [a7] | I. Mladenov, Phys. Lett. A , 137 (1989) pp. 313 |
Saxon-Hutner theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Saxon-Hutner_theorem&oldid=48612