Sample variance

sample dispersion

A scalar characteristic of the disperson, or spread, of a sample (consisting of real numbers) relative to a fixed point (called the centre of dispersion). It is numerically equal to the sum of the squares of the deviations of the values from . For real-valued random variables , the variable

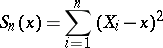is the sample variance about . The variables are often assumed to be independent and identically distributed in discussions about . Since, for any ,

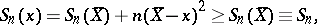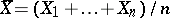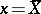where , the sample variance about will be minimal when . A small value of 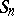indicates a concentration of the sample elements about and, conversely, a large value of 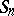indicates a large scattering of the sample elements. The concept of a sample variance extends to that of a sample covariance matrix for multivariate samples.

References

[1]	S.S. Wilks, "Mathematical statistics" , Wiley (1962)