Ringoid

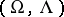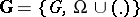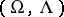A generalization of the notion of an associative ring (cf. Associative rings and algebras). Let be the variety of universal algebras (cf. also Universal algebra) of signature . The algebra is called a ringoid over the algebra of the variety , or an 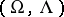-ringoid, if 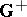belongs to 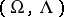, the algebra 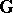is a subgroup with respect to the multiplication and the right distributive law holds with respect to multiplication:

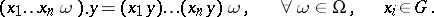The operations of are called the additive operations of the ringoi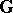d , and is called the additive algebra of the ringoid. A ringoid is called distributive if the left distributive law holds also, that is, if

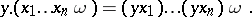An ordinary associative ring 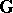is a distributive ringoid over an Abelian group (and 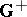is the additive group of 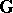). A ringoid over a group is called a near-ring, a ringoid over a semi-group a semi-ring, a ringoid over a loop a neo-ring. Rings over rings are also considered (under various names, one of which is Menger algebra).

References

[1]	A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)

Comments

The term "ringoid" , like groupoid, has at least two unrelated meanings, cf. [a1]–[a3].

References

[a1]	P.J. Hilton, W. Ledermann, "Homology and ringoids. I" Proc. Cambridge Phil. Soc. , 54 (1958) pp. 156–167
[a2]	P.J. Hilton, W. Ledermann, "Homology and ringoids. II" Proc. Cambridge Phil. Soc. , 55 (1959) pp. 149–164
[a3]	P.J. Hilton, W. Ledermann, "Homology and ringoids. III" Proc. Cambridge Phil. Soc. , 56 (1960) pp. 1–12