Riesz inequality

Let 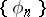be an orthonormal system of functions on an interval 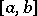and let 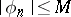almost everywhere on 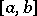for any .

a) If 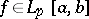, , 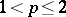then its Fourier coefficients with respect to ,

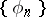satisfy the Riesz inequality

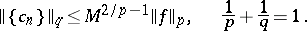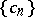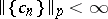b) For any sequence with , , there exists a function with 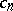as its Fourier coefficients and satisfying the Riesz inequality

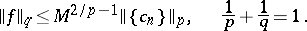If , , 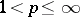then the conjugate function 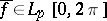and the Riesz inequality

holds, where is a constant depending only on .

Assertion 1) was for the first time proved by F. Riesz [1]; particular cases of it were studied earlier by W.H. Young and F. Hausdorff. Assertion 2) was first proved by M. Riesz [2].

References

[1]	F. Riesz, "Ueber eine Verallgemeinerung der Parsevalschen Formel" Math. Z. , 18 (1923) pp. 117–124
[2]	M. Riesz, "Sur les fonctions conjuguées" Math. Z. , 27 (1927) pp. 218–244
[3]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)
[4]	A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988)

Comments

For 2) see also Interpolation of operators (it is a consequence of the Marcinkiewicz interpolation theorem and the weak type of the conjugation operator) and [a3].

References

[a1]	P.L. Butzer, R.J. Nessel, "Fourier analysis and approximation" , 1 , Birkhäuser (1971) pp. Chapt. 8
[a2]	F. Hausdorff, "Eine Ausdehnung des Parsevalschen Satzes über Fourier-reihen" Math. Z. , 16 (1923) pp. 163–169
[a3]	E.M. Stein, G. Weiss, "Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1975) pp. Chapt. VI, §5