Riemann derivative
From Encyclopedia of Mathematics
Schwarzian derivative, second symmetric derivative, of a function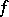 
at a point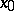 
The limit
 |
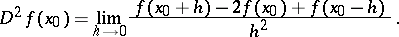It was introduced by B. Riemann in 1854, who proved that if at a point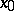 
the second derivative 
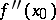exists, then so does the Riemann derivative and 
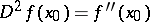. The upper and lower limits of
 |
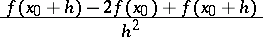as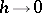 
are called the upper (
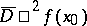) and lower (
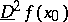) Riemann derivative, respectively.
Riemann derivatives find wide application in the theory of the representation of functions by trigonometric series, and in particular in connection with the Riemann summation method.
Comments
References
| [a1] | T.M. Apostol, "Mathematical analysis" , Blaisdell (1957) |
| [a2] | B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" , Gesammelte Math. Abhandlungen , Dover, reprint (1957) pp. 227–264 |
| [a3] | J. Wolff, "Fourier'sche Reihen" , Noordhoff (1931) |
How to Cite This Entry:
Riemann derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_derivative&oldid=48544
Riemann derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_derivative&oldid=48544
This article was adapted from an original article by T.P. Lukashenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article