Ribaucour congruence

A congruence of lines whose developable surfaces cut its mean surface by a conjugate net of lines. Let 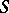be the mean surface of a Ribaucour congruence. Then there is a family of surfaces corresponding to 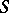by the orthogonality of the line elements, and having in each pair of corresponding points a normal parallel to a ray of the congruence. Conversely, if a pair of surfaces 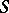and is given that correspond to each other by the orthogonality of the line elements, then the congruences formed by the rays passing through the points on 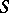and collinear to the normals of 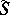at corresponding points are a Ribaucour congruence with mean surface 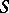. The surface 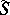is called the generating surface of the Ribaucour congruence. The curvature lines of correspond to those generating surfaces of the congruence whose lines of contraction intersect the ray in the centre. The developable surfaces of a Ribaucour congruence correspond to the asymptotic lines of the generating surface . The generating surface of a normal Ribaucour congruence is a minimal surface. This type of congruence is formed by the normals of a surface with the isothermic spherical image of curvature lines.

Such congruences were examined for the first time by A. Ribaucour in 1881.

References

[1]	S.P. Finikov, "Projective-differential geometry" , Moscow-Leningrad (1937) (In Russian)
[2]	S.P. Finikov, "Theorie der Kongruenzen" , Akademie Verlag (1959) (Translated from Russian)