Resolution of the identity
A one-parameter family  ,
,  , of orthogonal projection operators acting on a Hilbert space
, of orthogonal projection operators acting on a Hilbert space  , such that
, such that
1)  if
if  ;
;
2)  is strongly left continuous, i.e.
is strongly left continuous, i.e.  for every
for every  ;
;
3)  as
as 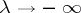 and
and 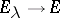 as
as 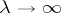 ; here 0 and
; here 0 and 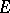 are the zero and the identity operator on the space
are the zero and the identity operator on the space 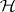 .
.
Condition 2) can be replaced by the condition of strong right continuity at every point 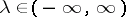 .
.
Every self-adjoint operator  acting on
acting on 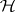 generates in a unique way a resolution of the identity. Here, in addition to 1)–3), the following conditions also hold:
generates in a unique way a resolution of the identity. Here, in addition to 1)–3), the following conditions also hold:
4) if 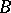 is a bounded operator such that
is a bounded operator such that 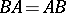 , then
, then 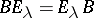 for any
for any 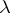 ;
;
5) if 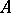 is a bounded operator and
is a bounded operator and 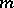 ,
, 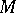 are its greatest lower and least upper bounds, respectively, then
are its greatest lower and least upper bounds, respectively, then
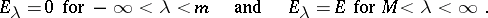 |
The resolution of the identity given by the operator 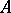 completely determines the spectral properties of that operator, namely:
completely determines the spectral properties of that operator, namely:
a) a point  is a regular point of
is a regular point of 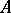 if and only if it is a point of constancy, that is, if there is a
if and only if it is a point of constancy, that is, if there is a 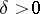 such that
such that 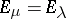 for
for 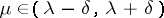 ;
;
b) a point 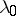 is an eigenvalue of
is an eigenvalue of 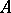 if and only if at this point
if and only if at this point 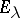 has a jump, that is,
has a jump, that is,  ;
;
g) if 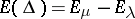 , then
, then 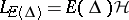 is an invariant subspace of
is an invariant subspace of 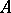 .
.
Hence the resolution of the identity determined by the operator 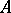 is also called the spectral function of this operator (cf. Spectral resolution).
is also called the spectral function of this operator (cf. Spectral resolution).
Conversely, every resolution of the identity 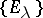 uniquely determines a self-adjoint operator
uniquely determines a self-adjoint operator 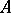 for which this resolution is the spectral function. The domain of definition
for which this resolution is the spectral function. The domain of definition 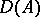 of
of  consists exactly of those
consists exactly of those  for which
for which
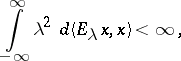 |
and there is a representation of 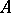 as an operator Stieltjes integral:
as an operator Stieltjes integral:
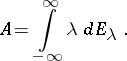 |
References
| [1] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
| [2] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in a Hilbert space" , 1–2 , F. Ungar (1961–1963) (Translated from Russian) |
| [3] | L.V. Kantorovich, G.P. Akilov, "Functional analysis in normed spaces" , Pergamon (1964) (Translated from Russian) |
Comments
To the property 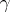 ) mentioned above one may add that the spectrum of the restriction of
) mentioned above one may add that the spectrum of the restriction of 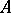 to
to 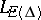 is contained in the set
is contained in the set 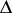 .
.
Resolution of the identity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Resolution_of_the_identity&oldid=48529