Representation with a highest weight vector
A linear representation (cf. Representation of a Lie algebra)  of a finite-dimensional semi-simple split Lie algebra
of a finite-dimensional semi-simple split Lie algebra  over a field
over a field  of characteristic zero with a split Cartan subalgebra
of characteristic zero with a split Cartan subalgebra  , having the following properties.
, having the following properties.
1) In the space  of
of  there is a cyclic vector
there is a cyclic vector  (i.e.
(i.e.  is the smallest
is the smallest  -invariant subspace containing
-invariant subspace containing  ).
).
2)  for all
for all  , where
, where 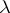 is some fixed linear form on
is some fixed linear form on  with values in
with values in  .
.
3) If  is a system of simple roots, defined by a lexicographical order on the set
is a system of simple roots, defined by a lexicographical order on the set 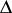 of all roots of
of all roots of  relative to
relative to 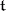 (cf. Root system), and if
(cf. Root system), and if  are the vectors from the Chevalley basis of
are the vectors from the Chevalley basis of 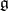 corresponding to
corresponding to  ,
, 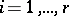 , then
, then 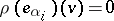 for all
for all  . Thus,
. Thus,  is a weight relative to the restriction of
is a weight relative to the restriction of 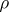 to
to 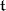 (cf. Weight of a representation of a Lie algebra); it is called a highest weight. The space
(cf. Weight of a representation of a Lie algebra); it is called a highest weight. The space 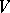 is called a cyclic
is called a cyclic  -module with highest weight
-module with highest weight 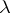 and generator
and generator  , and
, and  is called a highest weight vector.
is called a highest weight vector.
There exists for every linear form 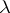 on
on  a unique, up to equivalence, irreducible representation
a unique, up to equivalence, irreducible representation  of
of  with highest weight
with highest weight 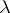 . The
. The  -module
-module 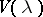 determined by
determined by 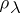 is a direct sum of weight subspaces relative to the restriction of
is a direct sum of weight subspaces relative to the restriction of  to
to  . Their weights have the form
. Their weights have the form
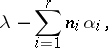 |
where the  are non-negative integers. The weight subspace
are non-negative integers. The weight subspace 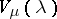 of weight
of weight  is finite-dimensional, spanned over
is finite-dimensional, spanned over  by vectors of the form
by vectors of the form
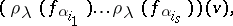 |
and for any 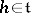 the restriction of
the restriction of  to
to 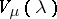 is the operator of scalar multiplication by
is the operator of scalar multiplication by 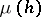 . The space
. The space 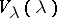 is one-dimensional; the weight
is one-dimensional; the weight 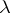 is the only highest weight of
is the only highest weight of 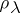 and can be characterized as the unique weight of the
and can be characterized as the unique weight of the 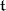 -module
-module  such that any other weight has the form
such that any other weight has the form
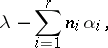 |
where the 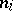 are non-negative integers.
are non-negative integers.
A representation  is finite-dimensional if and only if
is finite-dimensional if and only if  is a dominant linear form on
is a dominant linear form on 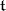 , i.e.
, i.e.  is a non-negative integer for
is a non-negative integer for  . Every irreducible finite-dimensional linear representation of
. Every irreducible finite-dimensional linear representation of 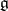 has the form
has the form  for some dominant linear form
for some dominant linear form  on
on  (hence all such representations are classified, up to equivalence, by the dominant linear forms on
(hence all such representations are classified, up to equivalence, by the dominant linear forms on 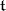 ). The set of all weights of a finite-dimensional representation
). The set of all weights of a finite-dimensional representation 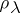 relative to
relative to 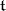 is invariant relative to the Weyl group of
is invariant relative to the Weyl group of  (regarded as a group of linear transformations of
(regarded as a group of linear transformations of  ), and if weights
), and if weights  and
and  belong to one orbit of the Weyl group, then the dimensions of the spaces
belong to one orbit of the Weyl group, then the dimensions of the spaces 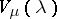 and
and  are equal. For every weight
are equal. For every weight 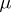 and every root
and every root 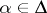 the number
the number 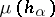 is an integer; if, moreover,
is an integer; if, moreover, 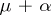 is also a weight, then
is also a weight, then
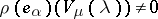 |
(here 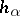 is the element in
is the element in  corresponding to
corresponding to 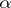 and
and  is the root vector of
is the root vector of  ).
).
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [2] | , Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Secr. Math. Univ. Paris (1955) |
| [3] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [4] | E. Cartan, "Les tenseurs irréductibles et les groupes linéaires simples et semi-simples" Bull. Sci. Math. , 49 (1925) pp. 130–152 |
| [5] | Harish-Chandra, "On some applications of the universal enveloping algebra of a semisimple Lie algebra" Trans. Amer. Math. Soc. , 70 (1951) pp. 28–96 |
Representation with a highest weight vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_with_a_highest_weight_vector&oldid=48523