Remainder

of an expansion of a function

An additive term in a formula approximating a function by another, simpler, function. The remainder equals the difference between the given function and its approximating function, and an estimate of it is therefore an estimate of the accuracy of the approximation.

The approximating formulas alluded to include the Taylor formula, interpolation formulas, asymptotic formulas, formulas for the approximate evaluation of some quantity, etc. Thus, in the Taylor formula

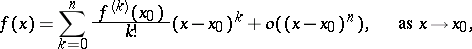the term 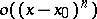is called the remainder (in Peano's form). Given the asymptotic expansion

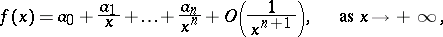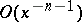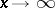of a function, the remainder is , as . In the Stirling formula, which gives an asymptotic expansion of the Euler gamma-function,

the remainder is .

Comments

The remainder of an integer upon division by a natural number 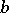is the number , , 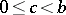for which with an integer. See also Remainder of an integer.

References

[a1]	N. Bleistein, R.A. Handelsman, "Asymptotic expansions of integrals" , Dover, reprint (1986) pp. Chapts. 1, 3, 5
[a2]	P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126
[a3]	M. Spivak, "Calculus" , Benjamin (1967)