Reidemeister torsion
de Rham torsion, Franz torsion
An invariant which allows one to distinguish many structures in differential topology, for example knots and smooth structures on manifolds, particularly on lens spaces. Reidemeister torsion was first introduced by K. Reidemeister (see [1]) while studying three-dimensional lenses, the generalization for  -dimensional lenses was obtained independently in [2] and [3].
-dimensional lenses was obtained independently in [2] and [3].
Let  be a free complex of left
be a free complex of left  -modules, where
-modules, where  is an associative ring with a unit element. Further, let
is an associative ring with a unit element. Further, let  be a matrix representation of
be a matrix representation of  , i.e. a homomorphism from
, i.e. a homomorphism from  into the ring
into the ring  of all real
of all real  -matrices. Let
-matrices. Let  be distinguished bases in the modules
be distinguished bases in the modules 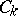 of the complex
of the complex 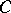 , and let the complex
, and let the complex  of
of  -modules be acyclic; then the Whitehead torsion is defined as
-modules be acyclic; then the Whitehead torsion is defined as  , where
, where  is the multiplicative group of the field of real numbers. The number
is the multiplicative group of the field of real numbers. The number  is called the Reidemeister torsion of the complex
is called the Reidemeister torsion of the complex  , and also the real Reidemeister torsion.
, and also the real Reidemeister torsion.
The usefulness of transforming the Whitehead torsion into the Reidemeister torsion is based on Bass' theorem [4]. If 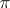 is a finite group, then the element
is a finite group, then the element  has finite order if
has finite order if  for any representation
for any representation  , where
, where  is the Reidemeister torsion induced by the element
is the Reidemeister torsion induced by the element 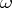 .
.
References
| [1] | K. Reidemeister, "Homotopieringe und Linsenräume" Abh. Math. Sem. Univ. Hamburg , 11 (1935) pp. 102–109 |
| [2] | W. Franz, "Ueber die Torsion einer Ueberdeckung" J. Reine Angew. Math. , 173 (1935) pp. 245–254 |
| [3] | G. de Rham, "Sur les nouveaux invariants de M. Reidemeister" Mat. Sb. , 1 : 5 (1936) pp. 737–743 |
| [4] | H. Bass, " -theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 5–60 -theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 5–60 |
Comments
References
| [a1] | J. Milnor, "Whitehead torsion" Bull. Amer. Math. Soc. , 72 (1966) pp. 358–426 |
Reidemeister torsion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reidemeister_torsion&oldid=48494