Regulated rewriting
An important branch of formal language theory, starting from the observation that most natural and artificial languages of interest are non-context-free (cf. Grammar, context-free). By imposing certain restrictions on the derivation in context-free grammars, the generative power is increased, still preserving some of the attractive features of context-free grammars.
There are some dozens of regulating mechanisms of this type: matrix, programmed, random context, regularly controlled, periodically time variant, indexed, state, valence, parallel grammars, grammars controlled by bicoloured digraphs, etc. See [a1] for details; recent information can be found in [a2].
Example.
A programmed grammar (introduced in [a3]) is a construct
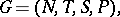 |
where 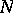 ,
, 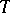 are disjoint alphabets (the non-terminal and the terminal alphabet),
are disjoint alphabets (the non-terminal and the terminal alphabet), 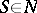 (axiom), and
(axiom), and 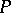 is a finite set of quadruples
is a finite set of quadruples 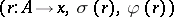 ;
; 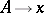 is a context-free rule over
is a context-free rule over 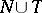 ,
,  is the label of the rule,
is the label of the rule, 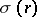 and
and 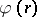 are sets of labels of rules in
are sets of labels of rules in 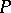 (
(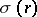 is the success field and
is the success field and 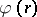 is the failure field). Let
is the failure field). Let 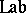 be the set of all labels of rules in
be the set of all labels of rules in 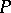 . For
. For  one writes
one writes 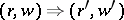 if one of the following two cases holds:
if one of the following two cases holds:
1)  and
and 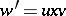 , for
, for 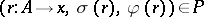 ,
, 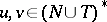 , and
, and 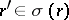 ;
;
2) 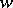 does not contain the symbol
does not contain the symbol 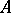 , for
, for  and
and 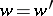 ,
, 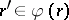 . (Note the way of controlling the sequencing of rules application by means of the mappings
. (Note the way of controlling the sequencing of rules application by means of the mappings 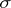 and
and 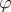 from
from  to the power set of
to the power set of 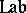 .) The language generated by
.) The language generated by  is
is
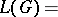 |
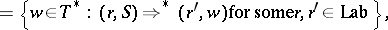 |
where 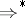 is the reflexive and transitive closure of the relation
is the reflexive and transitive closure of the relation 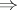 . Let
. Let 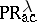 be the family of languages of this form; when
be the family of languages of this form; when 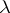 -rules are not allowed, one writes
-rules are not allowed, one writes 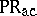 . When
. When 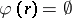 for all rules in
for all rules in 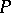 , one says that the grammar is without appearance checking; the corresponding families of languages are denoted by
, one says that the grammar is without appearance checking; the corresponding families of languages are denoted by  , PR. Denote by CF, CS, and RE the families of context-free, context-sensitive, and recursively enumerable languages, respectively. Then:
, PR. Denote by CF, CS, and RE the families of context-free, context-sensitive, and recursively enumerable languages, respectively. Then:
1) 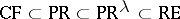 ,
, 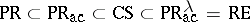 ;
;
2) 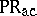 is an abstract family of languages (cf. also Trio).
is an abstract family of languages (cf. also Trio).
References
| [a1] | J. Dassow, Gh. Păun, "Regulated rewriting in formal language theory" , Springer (1989) |
| [a2] | J. Dassow, Gh. Păun, A. Salomaa, "Regulated rewriting" G. Rozenberg (ed.) A. Salomaa (ed.) , Handbook of Formal Languages , Springer (1997) |
| [a3] | D. Rosenkrantz, "Programmed grammars and classes of formal languages" J. ACM , 16 (1969) pp. 107 –131 |
Regulated rewriting. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regulated_rewriting&oldid=48492