Regular p-group
A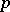 
-group 
such that for all 
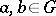and any integer 
an equality
 |
holds, where 
are elements of the commutator subgroup of the subgroup generated by the elements 
and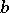 
. Subgroups and quotient groups of a regular 
-group are regular. A finite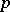 
-group 
is regular if and only if for all 
,
 |
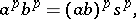where 
is an element of the commutator subgroup of the subgroup generated by 
and 
.
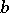The elements of the form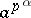 
, 
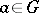, in a regular 
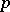-group 
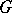form a characteristic subgroup, 
, and the elements of order at most 
form a fully-characteristic subgroup, 
.
Examples of regular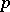 
-groups are 
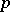-groups of nilpotency class at most 
, and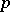 
-groups of order at most 
. For any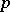 
, there is a non-regular 
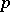-group 
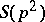of order 
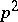(it is isomorphic to the wreath product of the cyclic group of order 
with itself).
References
| [1] | M. Hall, "Group theory" , Macmillan (1959) |
Regular p-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_p-group&oldid=48483