Regular linear system
of ordinary differential equations
A system of the form
 | (1) |
(where 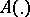 is a mapping
is a mapping 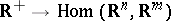 that is summable on every interval and has the property that
that is summable on every interval and has the property that
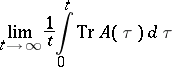 |
exists and is equal to 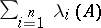 , where
, where 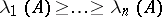 are the characteristic Lyapunov exponents (cf. Lyapunov characteristic exponent) of the system (1)).
are the characteristic Lyapunov exponents (cf. Lyapunov characteristic exponent) of the system (1)).
For a triangular system
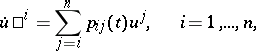 |
to be regular it is necessary and sufficient that the limits
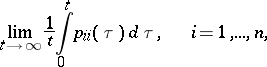 |
exist (Lyapunov's criterion). Every reducible linear system and every almost-reducible linear system is regular.
The role of the concept of a regular linear system is clarified by the following theorem of Lyapunov. Let the system (1) be regular and let 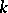 of its characteristic Lyapunov exponents be negative:
of its characteristic Lyapunov exponents be negative:
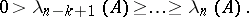 |
Then for every system
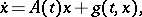 | (2) |
where 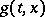 satisfies the following conditions:
satisfies the following conditions: 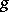 and
and 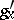 are continuous, and
are continuous, and 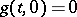 ,
, 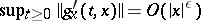 , where
, where 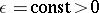 , there is a
, there is a 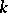 -dimensional manifold
-dimensional manifold 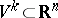 containing the point
containing the point 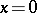 , such that every solution
, such that every solution 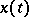 of (2) starting on
of (2) starting on 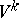 (i.e.
(i.e. 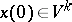 ) exponentially decreases as
) exponentially decreases as 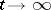 ; more precisely, for every
; more precisely, for every 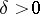 there is a
there is a 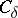 such that the inequality
such that the inequality
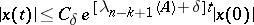 |
is satisfied.
References
| [1] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [2] | B.F. Bylov, R.E. Vinograd, D.M. Grobman, V.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian) |
| [3] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 : 1 (1976) pp. 46–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 : 1 (1974) pp. 71–146 |
Regular linear system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_linear_system&oldid=48482