Regular lattice
A conditionally-complete lattice in which the following condition (also called the axiom of regularity) holds: For any sequence 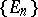 of bounded sets for which
of bounded sets for which
 |
there exist finite subsets  with the same property (where
with the same property (where  denotes convergence in order, cf. also Riesz space). Such lattices are most often met in functional analysis and in measure theory (for example, regular
denotes convergence in order, cf. also Riesz space). Such lattices are most often met in functional analysis and in measure theory (for example, regular 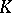 -spaces and Boolean algebras). They arise naturally in the problem of extending homomorphisms and positive linear operators. In a regular lattice the following two principles hold: a) the diagonal principle (if
-spaces and Boolean algebras). They arise naturally in the problem of extending homomorphisms and positive linear operators. In a regular lattice the following two principles hold: a) the diagonal principle (if 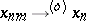 and
and 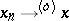 , then
, then 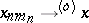 for some sequence of indices
for some sequence of indices 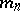 ); and b) the principle of countability of type (every bounded infinite set contains a countable subset with the same bounds). Conversely, a) and b) together imply the axiom of regularity. Examples of regular lattices are: Any
); and b) the principle of countability of type (every bounded infinite set contains a countable subset with the same bounds). Conversely, a) and b) together imply the axiom of regularity. Examples of regular lattices are: Any 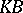 -space and, in particular, any
-space and, in particular, any 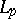 ,
,  ; the Boolean algebra of measurable sets modulo sets of measure 0 in an arbitrary space with a finite countably-additive measure. Other examples of regular Boolean algebras are based on the negation of the Suslin hypothesis.
; the Boolean algebra of measurable sets modulo sets of measure 0 in an arbitrary space with a finite countably-additive measure. Other examples of regular Boolean algebras are based on the negation of the Suslin hypothesis.
References
| [1] | L.V. Kantorovich, B.Z. Vulikh, A.G. Pinsker, "Functional analysis in semi-ordered spaces" , Moscow-Leningrad (1950) (In Russian) |
Comments
References
| [a1] | W.A.J. Luxemburg, A.C. Zaanen, "Theory of Riesz spaces" , I , North-Holland (1972) |
Regular lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_lattice&oldid=48481