Regular automorphism
An automorphism 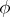 of a group
of a group  such that
such that  for every non-identity element
for every non-identity element 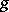 of
of  (that is, the image of every non-identity element of a group under a regular automorphism must be different from that element). If
(that is, the image of every non-identity element of a group under a regular automorphism must be different from that element). If 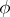 is a regular automorphism of a finite group
is a regular automorphism of a finite group  , then for every prime
, then for every prime 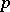 dividing the order of
dividing the order of  ,
, 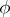 leaves invariant (that is, maps to itself) a unique Sylow
leaves invariant (that is, maps to itself) a unique Sylow 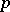 -subgroup
-subgroup  of
of  , and any
, and any 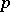 -subgroup of
-subgroup of 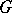 invariant under
invariant under 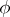 is contained in
is contained in  . A finite group that admits a regular automorphism of prime order is nilpotent (cf. Nilpotent group) [2]. However, there are solvable (cf. Solvable group) non-nilpotent groups admitting a regular automorphism of composite order.
. A finite group that admits a regular automorphism of prime order is nilpotent (cf. Nilpotent group) [2]. However, there are solvable (cf. Solvable group) non-nilpotent groups admitting a regular automorphism of composite order.
References
| [1] | D. Gorenstein, "Finite groups" , Chelsea, reprint (1980) |
| [2] | J.G. Thompson, "Finite groups with fixed-point-free automorphisms of prime order" Proc. Nat. Acad. Sci. , 45 (1959) pp. 578–581 |
Comments
A regular automorphism is also called a fixed-point-free automorphism.
Regular automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_automorphism&oldid=48478