Recurrent function
A function that is a recurrent point of the shift dynamical system. An equivalent definition is: A function  , where
, where  is a metric space, is called recurrent if it has a pre-compact set of values, is uniformly continuous and if for each sequence of numbers
is a metric space, is called recurrent if it has a pre-compact set of values, is uniformly continuous and if for each sequence of numbers  such that the limit
such that the limit
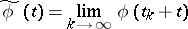 |
exists (the limit in the compact-open topology, i.e. uniformly on each segment) a sequence of numbers 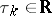 can be found such that
can be found such that
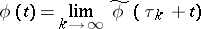 |
in the compact-open topology.
If  is a bounded uniformly-continuous function, then numbers
is a bounded uniformly-continuous function, then numbers  can be found such that the limit (in the compact-open topology)
can be found such that the limit (in the compact-open topology)
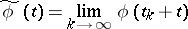 |
exists and is a recurrent function. Every almost-periodic function, and, in particular, every periodic function, is recurrent.
References
| [1] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 (1976) pp. 46–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146 |
Comments
A recurrent function is nothing but a point in a compact minimal set in a dynamical system of the form 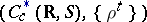 , where
, where 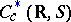 is the space of continuous functions
is the space of continuous functions  with
with  a pre-compact set in
a pre-compact set in 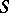 (
(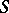 a metric space), endowed with the compact-open topology, and
a metric space), endowed with the compact-open topology, and 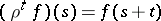 for
for 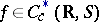 and
and 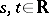 . In the case
. In the case  , this system is called the Bebutov system. In [a1], the recurrent functions (according to the above definition) are called minimal functions.
, this system is called the Bebutov system. In [a1], the recurrent functions (according to the above definition) are called minimal functions.
References
| [a1] | J. Auslander, F. Hahn, "Point transitive flows, algebras of functions and the Bebutov system" Fund. Math. , 60 (1967) pp. 117–137 |
Recurrent function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recurrent_function&oldid=48454