Ray function
A real-valued function 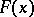 defined on an
defined on an  -dimensional space
-dimensional space 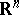 and satisfying the following conditions:
and satisfying the following conditions: 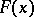 is continuous, non-negative and homogeneous (that is,
is continuous, non-negative and homogeneous (that is,  for any real number
for any real number  ). A ray function
). A ray function 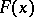 is said to be positive if
is said to be positive if 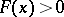 for all
for all  , and symmetric if
, and symmetric if  . A ray function is said to be convex if for any
. A ray function is said to be convex if for any 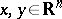 ,
,
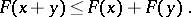 |
For any ray function 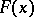 there is a constant
there is a constant  for which
for which
 |
If 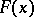 is positive, then there is also a constant
is positive, then there is also a constant 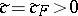 for which
for which
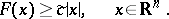 |
The set 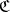 of points
of points  satisfying the condition
satisfying the condition
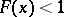 |
is a star body. Conversely, for any open star body 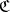 there is a unique ray function
there is a unique ray function 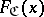 for which
for which
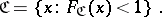 |
A star body 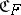 is bounded if and only if its ray function
is bounded if and only if its ray function 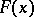 is positive. If
is positive. If 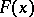 is a symmetric function, then
is a symmetric function, then 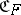 is symmetric about the point 0; the converse is also true. A star body is convex if and only if
is symmetric about the point 0; the converse is also true. A star body is convex if and only if 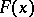 is a convex ray function.
is a convex ray function.
References
| [1] | J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1959) |
Comments
Star bodies are usually defined as closed ray sets. A ray function is more commonly called a distance function.
References
| [a1] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint) |
| [a2] | E. Hlawka, "Das inhomogene Problem in der Geometrie der Zahlen" , Proc. Internat. Congress Mathematicians (Amsterdam, 1954) , 3 , Noordhoff (1954) pp. 20–27 ((Also: Selecta, Springer 1990, 178–185.)) |
Ray function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ray_function&oldid=48442