Rank of a Lie algebra
The minimal multiplicity of the eigen value 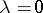 for the linear operators
for the linear operators 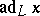 , where
, where  runs through the whole of the Lie algebra
runs through the whole of the Lie algebra 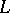 . It is assumed that
. It is assumed that 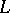 is a finite-dimensional algebra. An element
is a finite-dimensional algebra. An element  for which the multiplicity is minimal is called regular. The set of regular elements of a Lie algebra is open (in the Zariski topology). The rank of a Lie algebra is equal to the dimension of any Cartan subalgebra of it. The rank
for which the multiplicity is minimal is called regular. The set of regular elements of a Lie algebra is open (in the Zariski topology). The rank of a Lie algebra is equal to the dimension of any Cartan subalgebra of it. The rank 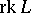 of a non-zero Lie algebra
of a non-zero Lie algebra 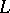 satisfies the inequalities
satisfies the inequalities
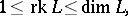 |
and equality 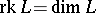 holds if and only if
holds if and only if 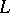 is nilpotent (cf. Lie algebra, nilpotent). For a semi-simple Lie algebra (cf. Lie algebra, semi-simple) over a field
is nilpotent (cf. Lie algebra, nilpotent). For a semi-simple Lie algebra (cf. Lie algebra, semi-simple) over a field 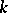 the rank coincides with the transcendence degree over
the rank coincides with the transcendence degree over 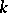 of the subfield of the field of rational functions on
of the subfield of the field of rational functions on 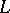 generated by all coefficients of the characteristic polynomials of the endomorphism
generated by all coefficients of the characteristic polynomials of the endomorphism 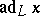 .
.
If 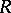 is the radical in
is the radical in 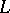 , then the rank of
, then the rank of 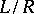 is called the semi-simple rank of the algebra
is called the semi-simple rank of the algebra 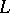 .
.
Examples. Let 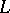 be one of the following Lie algebras: 1) the algebra
be one of the following Lie algebras: 1) the algebra 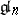 of all square matrices of order
of all square matrices of order  with elements from
with elements from 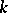 ; 2) the algebra
; 2) the algebra 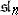 of all matrices with zero trace; 3) the algebra of all upper-triangular matrices; 4) the algebra of all diagonal matrices; or 5) the algebra of all upper-triangular matrices with zeros on the principal diagonal. For these algebras the ranks are
of all matrices with zero trace; 3) the algebra of all upper-triangular matrices; 4) the algebra of all diagonal matrices; or 5) the algebra of all upper-triangular matrices with zeros on the principal diagonal. For these algebras the ranks are  ,
, 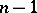 ,
,  ,
,  ,
, 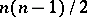 , and the semi-simple ranks are
, and the semi-simple ranks are 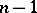 ,
, 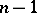 ,
,  ,
,  ,
,  .
.
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [2] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [3] | C. Chevalley, "Théorie des groupes de Lie" , 3 , Hermann (1955) |
Comments
References
| [a1] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) |
| [a2] | N. Bourbaki, "Eléments de mathématique. Groupes et algèbres de Lie" , Hermann (1975) pp. Chapt. 7 |
Rank of a Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_of_a_Lie_algebra&oldid=48432