Quotient category

A construct analogous to that of a quotient set or quotient algebra. Let be an arbitrary category, and suppose that an equivalence relation is given on its class of morphisms , satisfying the following conditions: 1) if , then the sources and targets of the morphisms and are the same; and 2) if , and if the product is defined, then . Let denote the equivalence class of 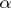. 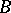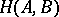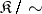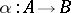The quotient category of by is the category (denoted by ) with the same objects as , and for any pair of objects , the set of morphisms in consists of the equivalence classes , where in ; multiplication of two morphisms and 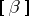is defined by the formula 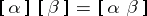(when the product is defined).

Every small category can be represented as a quotient category of the category of paths over an appropriate directed graph.

Comments

Any equivalence relation satisfying the conditions above is commonly called a congruence on (cf. Congruence (in algebra)).

References

[a1]	B. Mitchell, "Theory of categories" , Acad. Press (1965) pp. 4