Quaternary quadratic form
From Encyclopedia of Mathematics
A quadratic form in four variables. A quaternary quadratic form over a field 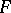 is related to the algebra of quaternions (cf. Quaternion) over the same field. Namely, corresponding to the algebra with basis
is related to the algebra of quaternions (cf. Quaternion) over the same field. Namely, corresponding to the algebra with basis  ,
,  ,
,  , and
, and  , is the quaternary quadratic form which is the norm of the quaternion,
, is the quaternary quadratic form which is the norm of the quaternion,
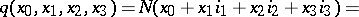 |
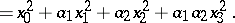 |
For quaternary quadratic forms corresponding to quaternion algebras, and only for these, composition of quaternary quadratic forms is defined:
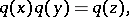 |
where the coordinates of the vector  are bilinear forms in
are bilinear forms in  and
and  . Composition of this kind is possible only for quadratic forms in two, four and eight variables.
. Composition of this kind is possible only for quadratic forms in two, four and eight variables.
Comments
The last-mentioned result is known as Hurwitz's theorem; see Quadratic form.
How to Cite This Entry:
Quaternary quadratic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quaternary_quadratic_form&oldid=48396
Quaternary quadratic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quaternary_quadratic_form&oldid=48396
This article was adapted from an original article by A.V. Malyshev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article