Quasi-symplectic space

A projective space of odd dimension, 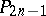, in which the following null-systems (cf. Zero system) are defined:

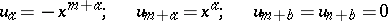and

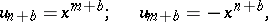The first null-system takes points in the space to hyperplanes passing through the 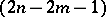-plane

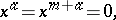while the second null-system takes points to points of this same plane.

The plane 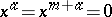is called the absolute, and the two null-systems are absolute null-systems of the quasi-symplectic space 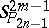. A quasi-symplectic space is a special case of a semi-symplectic space.

Collineations of 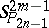taking the absolute plane to itself have the form

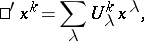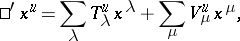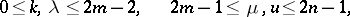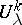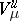and the matrices and are symplectic matrices of orders 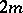and 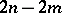; 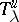is a rectangular matrix with 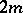columns and 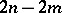rows.

These collineations are called quasi-symplectic transformations of 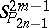. They commute with the given null-systems of the space. The quasi-symplectic invariant of two lines is defined by analogy with the symplectic invariant of lines of a symplectic space.

The quasi-symplectic space 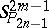can be obtained from the symplectic space 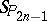by limit transition from the absolute of 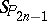to the absolute of 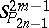. Namely, the first of the null-systems given takes all points of the space into planes passing through the absolute plane, while the second takes all planes into points of this same plane.

The quasi-symplectic transformations form a group, which is a Lie group.

References

[1]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)

References

[a1]	B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian)