Quasi-solution

A generalized solution of a certain ill-posed problem that (under sufficiently general conditions) satisfies, in contrast to a proper solution, the condition of being well-posed in the sense of Hadamard.

Let 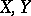be metric spaces, let 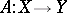and let 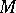be a subset of 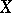. A quasi-solution of the equation

(1)

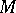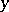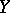on the set for given in is an element 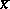in 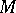that minimizes the residual 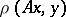for in 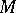. If equation (1) has a proper soluti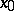on on 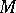, then 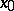is also quasi-solution.

The dependence of the set of quasi-solutions on 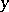is conveniently represented as a superposition of two mappings:

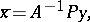where 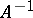is the (generally multi-valued) inverse of and 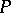is the metric projection operator in 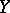onto the set 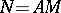. This superposition enables one to reduce the study of the properties of quasi-solutions to that of the mappings and 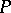. For example, if 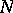is a Chebyshev set and 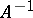is single-valued and continuous on 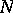, then the problem of finding a quasi-solution is well-posed. If 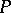or 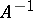is many-valued, then stability of the set 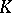can be formulated in terms of 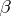-continuity (continuity of set-valued functions).

and 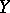are generally taken to be normed linear spaces, which enables one to obtain more complete and definitive results. Then the problem of finding quasi-solutions is well-posed if 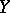is strictly convex, 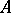is a continuous invertible linear operator and 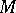is a convex compactum. There are a number of other combinations of conditions that ensure the well-posedness of the problem of finding quasi-solutions, in which some conditions are strengthened while others are weakened (for example, 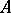is a closed linear operator but 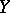is a Hilbert space).

There exists a number of methods for determining sets 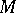that guarantee an effective determination of quasi-solutions. One of the most widespread methods consists in the following: One considers a third space 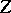(all or some of the spaces 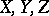may coincide) and a linear operator 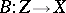for which 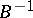is unbounded. One takes for the set 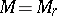the image of a ball

In this form the problem of finding a quasi-solution is a mathematical programming problem: To minimize the functional

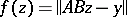subject to 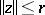. For Hilbert spaces and 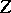one obtains a quadratic programming problem.

In the case of well-posedness of quasi-solutions, of great importance in applications are stability estimates, in which the dependence of 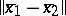on 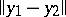is given. If the method for determining the set 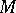is as described above, then stability of a quasi-solution is characterized by the function

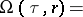The following relation holds:

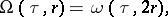where is the solution of the extremal problem .

For Hilbert spaces 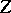and 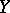there are expressions for in closed form.

References

[1]	V.K. Ivanov, "On linear problems which are not well-posed" Soviet Math. Dokl. , 4 : 3 (1962) pp. 981–983 Dokl. Akad. Nauk SSSR , 145 : 2 (1962) pp. 270–272
[2]	V.K. Ivanov, "On ill-posed problems" Mat. Sb. , 61 : 2 (1962) pp. 211–223 (In Russian)
[3]	O.A. Liskovets, "Stability of quasi-solutions of equations with a closed operator" Diff. Eq. , 7 : 9 (1971) pp. 1300–1303 Differentsial. Uravn. , 7 : 9 (1971) pp. 1707–1709
[4]	V.A. Morozov, "Linear and nonlinear ill-posed problems" J. Soviet Math. , 4 : 6 (1975) pp. 706–755 Itogi Nauk. i Tekhn. Mat. Anal. , 11 (1973) pp. 129–178
[5]	A.N. Tikhonov, V.I. [V.I. Arsenin] Arsenine, "Solution of ill-posed problems" , Wiley (1977) (Translated from Russian)
[6]	V.I. Krylov, V.V. Bobkov, P.I. Monastyrnyi, "Computing methods of higher mathematics" , 1–2 , Minsk (1972–1975) (In Russian)

Comments

Frequently the operator 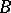is such that is a differential operator. On a suitable space, 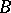is then a compact operator, so that the set is a compactum.

References

[a1]	B. Hofmann, "Regularization for applied inverse and ill-posed problems" , Teubner (1986)
[a2]	C.W. Groetsch, "The theory of Tikhonov regularization for Fredholm equations of the first kind" , Pitman (1984)
[a3]	J. Baumeister, "Stable solution of inverse problems" , Vieweg (1987)
[a4]	M.Z. Nashed (ed.) , Genealized inverses and applications , Acad. Press (1976)
[a5]	V.A. Morozov, "Methods for solving incorrectly posed problems" , Springer (1984) (Translated from Russian)