Quasi-regular radical
of a ring
The largest quasi-regular ideal of the given ring. An ideal 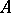 of a ring
of a ring 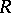 is called quasi-regular if
is called quasi-regular if 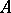 is a quasi-regular ring. There exists in every alternative (in particular, associative) ring a quasi-regular radical; it coincides with the sum of all right (left) quasi-regular ideals (see [1], [10]). The quasi-regular radical of an associative ring is also called the Jacobson radical.
is a quasi-regular ring. There exists in every alternative (in particular, associative) ring a quasi-regular radical; it coincides with the sum of all right (left) quasi-regular ideals (see [1], [10]). The quasi-regular radical of an associative ring is also called the Jacobson radical.
The quasi-regular radical 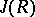 of an arbitrary alternative ring
of an arbitrary alternative ring 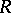 is equal to the intersection of all maximal modular right (left) ideals of
is equal to the intersection of all maximal modular right (left) ideals of 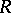 ;
; 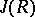 is also equal to the intersection of the kernels of all irreducible right (left) representations of
is also equal to the intersection of the kernels of all irreducible right (left) representations of 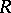 (see [1], [5]–[8]). A ring
(see [1], [5]–[8]). A ring 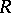 is called
is called 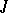 -semi-simple if
-semi-simple if 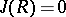 . The quotient ring
. The quotient ring 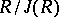 is always semi-simple. Every semi-simple ring is isomorphic to a subdirect sum of primitive rings [1], [8]. If
is always semi-simple. Every semi-simple ring is isomorphic to a subdirect sum of primitive rings [1], [8]. If 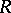 satisfies the minimum condition for right (left) ideals, then the radical
satisfies the minimum condition for right (left) ideals, then the radical 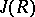 is nilpotent and the quotient ring
is nilpotent and the quotient ring 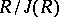 is isomorphic to a finite direct sum of complete matrix rings over skew-fields and Cayley–Dickson algebras (the latter terms are absent in the associative case), see [1]–[3]. Let
is isomorphic to a finite direct sum of complete matrix rings over skew-fields and Cayley–Dickson algebras (the latter terms are absent in the associative case), see [1]–[3]. Let  be a two-sided ideal of the ring
be a two-sided ideal of the ring 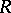 ; then
; then
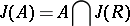 |
(see [1], [4]); if 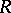 is an associative ring and
is an associative ring and 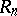 is the ring of matrices of order
is the ring of matrices of order  over
over 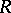 , then
, then
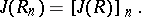 |
If 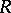 is an associative algebra over a field
is an associative algebra over a field 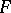 and the cardinality of
and the cardinality of 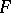 is greater than the dimension of
is greater than the dimension of 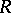 over
over 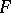 or if
or if 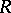 is algebraic over
is algebraic over 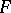 , then
, then 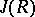 is a nil ideal. A quasi-regular radical of a finitely-generated alternative ring satisfying an essential identity relation is the same as a lower nil radical (see Radical of rings and algebras) [6]. Certain analogues of quasi-regular radicals exist in Jordan algebras (cf. Jordan algebra).
is a nil ideal. A quasi-regular radical of a finitely-generated alternative ring satisfying an essential identity relation is the same as a lower nil radical (see Radical of rings and algebras) [6]. Certain analogues of quasi-regular radicals exist in Jordan algebras (cf. Jordan algebra).
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [2] | K.A. Zhevlakov, "On radical ideals of an alternative ring" Algebra i Logika , 4 : 4 (1965) pp. 87–102 (In Russian) |
| [3] | K.A. Zhevlakov, "Alternative Artinian rings" Algebra i Logika , 5 : 3 (1966) pp. 11–36 (In Russian) |
| [4] | K.A. Zhevlakov, "On the Kleinfeld and Smiley radicals of alternative rings" Algebra and Logic , 8 : 2 (1969) pp. 100–102 Algebra i Logika , 8 : 2 (1969) pp. 176–180 |
| [5] | K.A. Zhevlakov, "Coincidence of Kleinfeld and Smiley radicals in alternative rings" Algebra and Logic , 8 : 3 (1969) pp. 175–181 Algebra i Logika , 8 : 3 (1969) pp. 309–319 |
| [6] | K.A. Zhevlakov, "Quasiregular ideals in finitely generated alternative rings" Algebra and Logic , 11 : 2 (1972) pp. 94–100 Algebra i Logika , 11 : 2 (1972) pp. 140–1161 |
| [7] | A.M. Slin'ko, I.P. Shestakov, "Right representation of algebras" Algebra and Logic , 13 : 5 (1973) pp. 312–333 Algebra i Logika , 13 : 5 (1974) pp. 544–588 |
| [8] | E. Kleinfeld, "Primitive alternative rings and semi-simplicity" Amer. J. Math. , 77 (1955) pp. 725–730 |
| [9] | K. McCrimmon, "The radical of a Jordan algebra" Proc. Nat. Acad. Sci. USA , 62 (1969) pp. 671–678 |
| [10] | M.F. Smiley, "The radical of an alternative ring" Ann. of Math. , 49 : 3 (1948) pp. 702–709 |
Comments
The radical of a row-finite infinite matrix ring is determined by annihilating sequences of ideals [a1]. The radical of a polynomial ring 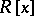 is
is 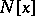 for some nil ideal
for some nil ideal 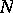 in
in 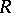 (the determination of
(the determination of 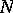 is an open problem).
is an open problem).
References
| [a1] | N.E. Sexauer, J.E. Warnock, "The radical of the row-finite matrices over an arbitrary ring" Trans. Amer. Math. Soc. , 39 (1969) pp. 281–295 |
| [a2] | L.H. Rowen, "Ring theory" , I, II , Acad. Press (1988) |
Quasi-regular radical. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-regular_radical&oldid=48393