Quasi-periodic function
with periods 
A function 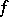 such that
such that 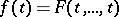 for some continuous function
for some continuous function 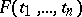 of
of  variables that is periodic with respect to
variables that is periodic with respect to  with periods
with periods  , respectively. All the
, respectively. All the  are required to be strictly positive and their reciprocals
are required to be strictly positive and their reciprocals  have to be rationally linearly independent. If
have to be rationally linearly independent. If  and
and 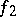 are continuous periodic functions with periods
are continuous periodic functions with periods 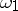 and
and 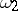 , respectively, where
, respectively, where  is irrational, then
is irrational, then 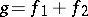 and
and 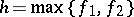 are quasi-periodic functions.
are quasi-periodic functions.
The theory of quasi-periodic functions serves as a basis for the creation of the theory of almost-periodic functions (cf. Almost-periodic function). In the case of continuous functions, quasi-periodic functions are a generalization of periodic functions, but a particular case of almost-periodic functions.
Quasi-periodic functions have a representation
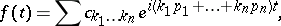 |
where the 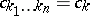 are such that
are such that 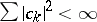 . Quasi-periodic functions possess the following properties: addition and multiplication of quasi-periodic functions yield quasi-periodic functions; a sequence of quasi-periodic functions that is uniformly convergent for
. Quasi-periodic functions possess the following properties: addition and multiplication of quasi-periodic functions yield quasi-periodic functions; a sequence of quasi-periodic functions that is uniformly convergent for 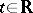 gives in the limit an almost-periodic function; if
gives in the limit an almost-periodic function; if 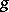 is an almost-periodic function and
is an almost-periodic function and 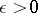 , then there exists a quasi-periodic function
, then there exists a quasi-periodic function 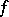 such that
such that
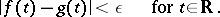 |
References
| [1] | P. Bohl, "Über die Darstellung von Funktionen einer Variabeln durch trigonometrische Reihen mit mehreren einer Variabeln proportionalen Argumenten" , Dorpat (1893) (Thesis) |
| [2] | V.Kh. Kharasakhal, "Almost-periodic solutions of ordinary differential equations" , Alma-Ata (1970) (In Russian) |
Comments
Quasi-periodic functions of time occur naturally in Hamiltonian mechanics to describe multi-periodic motions of integrable systems (see [a1] and Quasi-periodic motion).
Consider Hill's differential equation
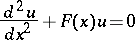 | (a1) |
with periodic 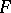 ,
, 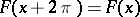 . A particular case is Mathieu's differential equation
. A particular case is Mathieu's differential equation
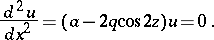 | (a2) |
A solution of (a1) need not be periodic. However, there is always a particular solution of the form 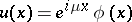 with
with 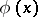 periodic (Floquet's theorem; cf. [a1] for a more precise statement). If the characteristic exponent
periodic (Floquet's theorem; cf. [a1] for a more precise statement). If the characteristic exponent 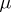 is real,
is real, 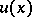 is a quasi-periodic function.
is a quasi-periodic function.
References
| [a1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [a2] | P.G. Bohl, "Ueber eine Differentialgleichung der Störungstheorie" Crelles J. , 131 (1906) pp. 268–321 |
| [a3] | B.M. Levitan, V.V. Zhikov, "Almost periodic functions and differential equations" , Cambridge Univ. Press (1984) pp. 47–48 (Translated from Russian) |
| [a4] | W. Magnus, S. Winkler, "Hill's equation" , Dover, reprint (1979) pp. 4ff |
Quasi-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-periodic_function&oldid=48391