Quasi-normal space
A regular space in which two disjoint  -sets have disjoint neighbourhoods. Every
-sets have disjoint neighbourhoods. Every  -space in which any two disjoint
-space in which any two disjoint  -sets have disjoint neighbourhoods is a quasi-normal space. Only for the quasi-normal spaces does the Stone–Čech compactification
-sets have disjoint neighbourhoods is a quasi-normal space. Only for the quasi-normal spaces does the Stone–Čech compactification  coincide with the space
coincide with the space  . The following theorem provides a large supply of non-normal quasi-normal spaces: The product of any number of separated metric spaces is quasi-normal.
. The following theorem provides a large supply of non-normal quasi-normal spaces: The product of any number of separated metric spaces is quasi-normal.
References
| [1] | V.I. Zaitsev, "Projection spectra" Trans. Moscow Math. Soc. , 27 (1972) pp. 135–199 Trudy Moskov. Mat. Obshch. , 27 (1972) pp. 129–193 |
| [2] | E.V. Shchepin, "On the bicompact Ponomarev–Zaicev extension and the so-called spectral parasite" Math. USSR Sb. , 17 (1972) pp. 317–326 Mat. Sb. , 88 : 2 (1972) pp. 316–325 |
Comments
Quasi-normal spaces arose in the study of the spectrum of a topological space (cf. also Spectrum of spaces). This spectrum is obtained as follows. A partition of a space  is a finite collection
is a finite collection  of canonical closed sets (cf. Canonical set) that covers
of canonical closed sets (cf. Canonical set) that covers  and the elements of which have disjoint interiors. The set of all these partitions is partially ordered by:
and the elements of which have disjoint interiors. The set of all these partitions is partially ordered by:  if and only if
if and only if 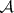 refines
refines  . The nerve
. The nerve 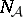 of
of 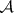 (cf. Nerve of a family of sets) is the complex of subfamilies of
(cf. Nerve of a family of sets) is the complex of subfamilies of 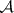 that have a non-empty intersection. There is an obvious simplicial mapping
that have a non-empty intersection. There is an obvious simplicial mapping 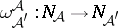 if
if 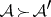 . If the set of partitions of
. If the set of partitions of 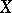 is (upward) directed by
is (upward) directed by 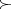 , then the inverse spectrum
, then the inverse spectrum  is the spectrum of
is the spectrum of 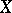 and is denoted by
and is denoted by 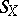 . To obtain a suitable limit of this spectrum one takes the set
. To obtain a suitable limit of this spectrum one takes the set 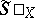 of maximal threads of
of maximal threads of  . A thread is a choice
. A thread is a choice 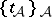 of simplexes with
of simplexes with 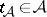 for all
for all  and such that
and such that 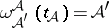 whenever
whenever 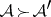 . A thread
. A thread  is maximal if whenever
is maximal if whenever 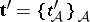 is another thread such that
is another thread such that 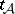 is a face of
is a face of 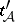 for every
for every 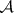 , one has
, one has 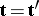 . The basic open sets are the sets of the form
. The basic open sets are the sets of the form  .
.
The space  , first introduced in [a3], is the space of all maximal centred systems of canonical closed sets topologized in the usual way, i.e. by taking the collection
, first introduced in [a3], is the space of all maximal centred systems of canonical closed sets topologized in the usual way, i.e. by taking the collection  as a base for the closed sets of
as a base for the closed sets of 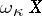 , where
, where 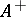 is the set of maximal centred systems to which
is the set of maximal centred systems to which 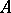 belongs.
belongs.
It turns out that there is a natural homeomorphism from 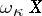 onto
onto 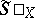 . Thus, for quasi-normal spaces
. Thus, for quasi-normal spaces  one has
one has 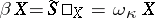 .
.
A 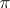 -set is a finite intersection of closures of open sets. A
-set is a finite intersection of closures of open sets. A  -space, first introduced in [1], is a semi-regular (
-space, first introduced in [1], is a semi-regular (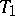 -) space all open sets of which are unions of
-) space all open sets of which are unions of 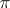 -sets. I.e., a
-sets. I.e., a 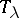 -space is a semi-regular (
-space is a semi-regular ( -) space (the canonical open sets form a base for the topology) in which the canonical closed sets form a net (of sets in a topological space), i.e. if
-) space (the canonical open sets form a base for the topology) in which the canonical closed sets form a net (of sets in a topological space), i.e. if 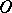 is open and
is open and 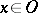 , then there is a canonical closed set
, then there is a canonical closed set  such that
such that 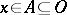 .
.
References
| [a1] | A. Kurosh, "Kombinatorischer Aufbau der bikompakten topologischen Räume" Compositio Math. , 2 (1935) pp. 471–476 |
| [a2] | V.I. Zaitsev, "Finite spectra of topological spaces and their limit spaces" Math. Ann. , 179 (1968–1969) pp. 153–174 |
| [a3] | V.I. Ponomarev, "Paracompacta: their projection spectra and continuous mappings" Mat. Sb. , 60 (102) (1963) pp. 89–119 (In Russian) |
Quasi-normal space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-normal_space&oldid=48390