Quasi-linearization

A collection of methods for the numerical solution of non-linear problems by reducing them to a sequence of linear problems. Lying at the basis of the apparatus of quasi-linearization is the Newton method and its generalization to function spaces, the theory of differential inequalities (cf. Differential inequality) and the method of dynamic programming. The simplest example illustrating a method of quasi-linearization is the use of the Newton–Raphson method for finding the root of a scalar monotone-decreasing strictly-convex function . In case the original non-linear function is approximated at each stage of the iteration process by a linear function , the root of is found, which serves as the next approximation, so that

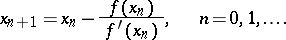Under fairly general conditions the sequence so constructed has the property of monotonicity and quadratic convergence:

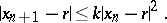The application of quasi-linearization to solving the Riccati equation

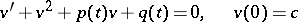(it is assumed that a solution exists on an interval 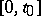), is as follows. The original equation is replaced by the equivalent equation

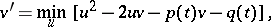where the minimum is taken over all functions defined on 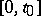. This equation has a number of properties inherent to linear equations, and in order to solve it one uses the linear differential equation

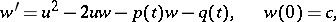where is a fixed function. By appealing to the property 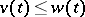(equality holding when ), one can construct a system of successive approximations

satisfying the linear equations

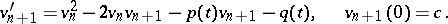The same recurrence relation can be obtained by applying the Newton–Kantorovich method (cf. Kantorovich process) to the original non-linear equation.

The employment of a quasi-linearization scheme in the solution of boundary value problems for the non-linear second-order differential equation

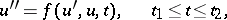leads to a sequence of functions 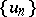satisfying the linear equations

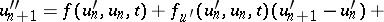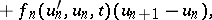with the linearized boundary conditions

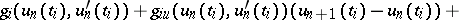The existence, uniqueness and quadratic convergence of the sequence follows from the corresponding convexity of the functions 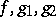over a sufficiently small interval .

The method of quasi-linearization finds application in the solution of two-point and multi-point boundary value problems for linear and non-linear ordinary differential equations, boundary value problems for elliptic and parabolic partial differential equations, variational problems, differential-difference and functional-differential equations, etc. As with every iteration scheme, the method of quasi-linearization is suitable for computer implementation and has various modifications enabling one to accelerate the convergence for narrower classes of problems. There exists a variety of examples of its use as a heuristic method for solving a number of problems in physics, technology and economy.

References

[1]	R.E. Bellman, R.E. Kalaba, "Quasilinearization and nonlinear boundary-value problems" , Elsevier (1965) (Translated from Russian)

References

[a1]	R. Bellman, G. Adomian, "Partial differential equations" , Reidel (1985) pp. Chapt. IV
[a2]	R. Bellman, R. Vasudevan, "Wave propagation. An invariant imbedding approach" , Reidel (1986)