Quasi-isometric spaces
From Encyclopedia of Mathematics
Metric spaces (cf. Metric space)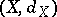 
and 
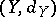, for which there exist two mappings 
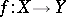and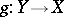 
and two constants 
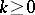and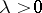 
such that for all 
and 
in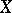 
and for all 
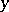and 
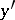in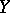 
, the following four inequalities hold:
 |
 |
 |
 |
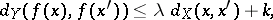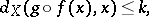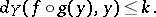This definition appears in [a1], where it is attributed to G.A. Margulis. The relation "X is quasi-isometric to Y" is an equivalence relation between metric spaces.
See also Quasi-isometry.
References
| [a1] | E. Ghys, "Les groupes hyperboliques" Astérisque , 189–190 (1990) pp. 203–238 (Sém. Bourbaki Exp. 722) |
How to Cite This Entry:
Quasi-isometric spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-isometric_spaces&oldid=48386
Quasi-isometric spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-isometric_spaces&oldid=48386
This article was adapted from an original article by A. Papadopoulos (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article