Quasi-elliptic space

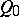A projective -space whose projective metric is defined by an absolute consisting of an imaginary cone (the absolute cone ) with an 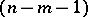-vertex (the absolute plane 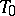) together with an imaginary 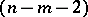-quadric 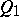on this 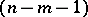-plane (the absolute quadric 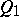); it is denoted by the symbol 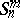, 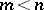. A quasi-elliptic space is of more general projective type in comparison with a Euclidean space and a co-Euclidean space; the metrics of the latter are obtained from those of the former. A quasi-elliptic space is a particular case of a semi-elliptic space. For 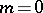, the absolute cone is a pair of coincident 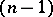-planes coinciding with the 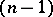-absolute plane 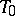, while the absolute coincides with the absolute of Euclidean -space. 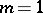For , the cone 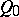is a cone with a point vertex and the absolute in this case is the same as that of the co-Euclidean -space. When 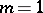, the cone 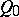is a pair of imaginary 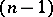-planes. In particular, the cone 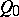of the quasi-elliptic three-space 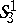is a pair of imaginary two-planes, the line (the 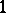-plane) 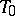is the real line of their intersection, while the quadric 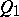is a pair of imaginary points on .

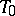The distance 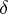between two points 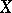and 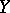is defined in case the line 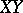does not intersect the 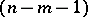-plane 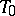by the relation

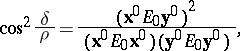where

are the vectors of the points 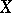and 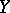, 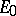is the linear operator defining the scalar product in the space of these vectors and is a real number; in case 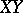intersects 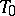, the distance 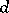between these points is defined by means of the distance between the vectors of the points 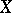and :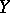

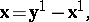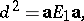where 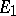is the linear operator defining the scalar product in the space of these vectors.

The angle between two planes whose -plane of intersection does not intersect the -plane 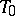is defined as the (normalized) distance between the corresponding points in the dual quasi-elliptic space 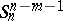, in which the coordinates are numerically equal or proportional to the projective coordinates of the planes in 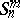. If the 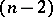-plane of intersection of two given planes intersects the 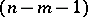-plane 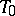, then the angle between the planes is in this case again defined by the numerical distance. When 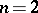the angles between the planes are the angles between the lines.

The motions of the quasi-elliptic space 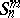are the collineations of this space that take the cone 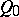into the plane 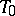and the quadric 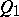into itself. The group of motions is a Lie group and the motions are described by orthogonal operators. In the quasi-elliptic space 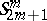, which is self-dual, co-motions are defined as the correlations that take each pair of points into two 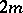-planes the angle between which is proportional to the distance between the points, and each pair of 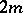-planes into two points the distance between which is proportional to the angle between the planes. The motions and co-motions of 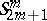form a group, which is a Lie group. The geometry of the -plane 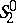is Euclidean geometry, while the geometry of the -plane 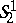is the same as that of the co-Euclidean plane.

The geometry of the -space 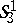is defined by an elliptic projective metric on lines that is co-Euclidean on planes and Euclidean in bundles of planes. The geometry of the -space 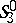is Euclidean, while the geometry of the -space 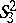is the same as that of the co-Euclidean -space. The space 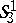with radius of curvature 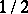is isometric to the connected group of motions of the Euclidean -space with a specially introduced metric. The connected group of motions of the quasi-Euclidean space 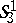is isomorphic to the direct product of two connected groups of motions of the Euclidean -plane.

References

[1]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)

References

[a1]	B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian)
[a2]	O. Giering, "Vorlesungen über höhere Geometrie" , Vieweg (1982)