Quadrature-sum method
A method for approximating an integral operator by constructing numerical methods for the solution of integral equations. The simplest version of a quadrature-sum method consists in replacing an integral operator, for instance of the form
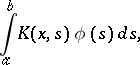 |
in an integral equation
 |
by an operator with finite-dimensional range, according to the rule
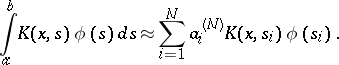 | (1) |
The integral equation, in turn, is approximated by the linear algebraic equation
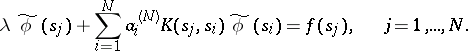 |
On the right-hand side of the approximate equation (1) is a quadrature formula for the integral with respect to  . Various generalizations of (1) are possible:
. Various generalizations of (1) are possible:
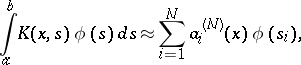 | (2) |
where the  are certain functions constructed from the kernel
are certain functions constructed from the kernel 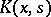 . The quadrature-sum method as generalized in the form (2) can be applied for the approximation of integral operators with singularities in the kernel and even of singular integral operators.
. The quadrature-sum method as generalized in the form (2) can be applied for the approximation of integral operators with singularities in the kernel and even of singular integral operators.
References
| [1] | L.V. Kantorovich, V.I. Krylov, "Approximate methods of higher analysis" , Noordhoff (1958) (Translated from Russian) MR0106537 Zbl 0083.35301 |
Comments
References
| [a1] | C.T.H. Baker, "The numerical treatment of integral equations" , Clarendon Press (1977) pp. Chapt. 4 MR0467215 Zbl 0373.65060 |
Quadrature-sum method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quadrature-sum_method&oldid=48363