Pseudo-tensor

A tensor considered up to multiplication by an arbitrary function (cf. Tensor on a vector space).

Comments

More precisely, a pseudo-tensor (also called relative tensor) is a quantity 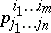which under a coordinate change transforms as

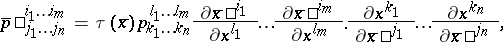where is a scalar-valued function. Most frequently (in applications), the function depends in a simple manner on the Jacobian determinant of the coordinate transformation. In [a1] the following cases are distinguished:

i) 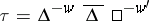, a tensor 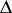-density of weight 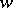and anti-weight ;

ii) 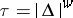, a tensor density of weight ;

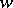iii) , a 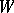-tensor.

Here is the complex conjugate of 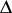. A tensor density of weight zero is an ordinary tensor (cf. Tensor on a vector space).

In [a2] a tensor 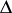-density of weight 1 and anti-weight 0 is called a tensor density and a tensor 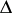-density of weight 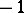and anti-weight 0 a tensor capacity.

References

[a1]	J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) pp. 11ff (Translated from German)
[a2]	R. Sauer (ed.) I. Szabó (ed.) , Mathematische Hilfsmittel des Ingenieurs , III , Springer (1968) pp. Sect. G.II.6