Pseudo-periodic function
From Encyclopedia of Mathematics
with periods 
A function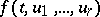 
of 
variables satisfying:
 |
 |
 |
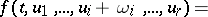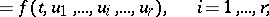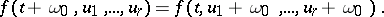Example: if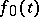 
and 
are continuous periodic functions with periods 
and 
, respectively, then 
is a pseudo-periodic function.
A pseudo-periodic function is connected with a quasi-periodic function and is determined by it in a unique way: A function 
is quasi-periodic with periods 
if and only if there exists a continuous pseudo-periodic function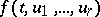 
with periods 
such that 
.
Comments
The expression "pseudo-periodic function" is also used to indicate a function with a pseudo-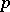
-period: 
for some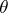 
and all 
. For such a function 
the function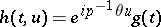 
is pseudo-periodic in the sense above.
References
| [a1] | M. Urabe, "Green functions of pseudo-periodic differential operators" M. Urabe (ed.) , Japan-United States Sem. Ordinary Differential and Functional Eq. , Springer (1971) pp. 106–122 |
| [a2] | J.A. Goldstein, "Asymptotics for bounded semigroups on Hilbert space" R. Nagel (ed.) et al. (ed.) , Aspects of Positivity in Funct. Anal. , North-Holland (1986) pp. 49–62 |
How to Cite This Entry:
Pseudo-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-periodic_function&oldid=48350
Pseudo-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-periodic_function&oldid=48350
This article was adapted from an original article by Yu.V. Komlenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article