Prolongation of solutions of differential equations
The property of solutions of ordinary differential equations to be extendible to a larger interval of the independent variable. Let
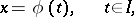 | (1) |
be a solution of the system
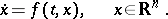 | (2) |
A solution 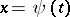 ,
, 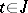 , is called a prolongation of the solution (1) if
, is called a prolongation of the solution (1) if 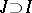 and
and 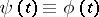 for
for 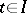 .
.
Suppose that the function
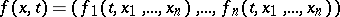 |
is defined in a domain  and suppose
and suppose 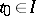 . The solution (1) is called indefinitely extendible (indefinitely extendible forwards (to the right), indefinitely extendible backward (to the left)) if a prolongation of it exists defined on the axis
. The solution (1) is called indefinitely extendible (indefinitely extendible forwards (to the right), indefinitely extendible backward (to the left)) if a prolongation of it exists defined on the axis 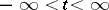 (respectively, on the semi-axis
(respectively, on the semi-axis 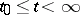 , on the semi-axis
, on the semi-axis 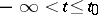 ). The solution (1) is called extendible forwards (to the right) up to the boundary
). The solution (1) is called extendible forwards (to the right) up to the boundary 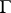 of
of 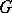 if a prolongation
if a prolongation 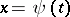 ,
, 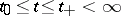 , of it exists with the following property: For any compact set
, of it exists with the following property: For any compact set 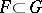 there is a value
there is a value 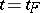 ,
, 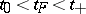 , such that the point
, such that the point 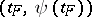 does not belong to
does not belong to 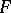 . Extendibility backward (to the left) up to the boundary
. Extendibility backward (to the left) up to the boundary 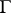 is defined analogously. A solution that cannot be extended is called non-extendible.
is defined analogously. A solution that cannot be extended is called non-extendible.
If the function 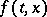 is continuous in
is continuous in 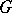 , then every solution (1) of (2) can be either extended forwards (backward) or indefinitely or up to the boundary
, then every solution (1) of (2) can be either extended forwards (backward) or indefinitely or up to the boundary 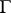 . In other words, every solution of (2) can be extended to a non-extendible solution. If the partial derivatives
. In other words, every solution of (2) can be extended to a non-extendible solution. If the partial derivatives
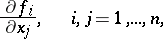 | (3) |
are continuous in 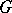 , then such a prolongation is unique.
, then such a prolongation is unique.
An interval 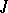 is called a maximal interval of existence of a solution of (2) if the solution cannot be extended to a larger interval. For any solution of a linear system
is called a maximal interval of existence of a solution of (2) if the solution cannot be extended to a larger interval. For any solution of a linear system
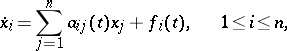 |
with coefficients 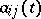 and right-hand sides
and right-hand sides 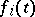 ,
, 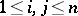 , that are continuous on an interval
, that are continuous on an interval 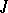 , the maximal interval of existence of a solution coincides with
, the maximal interval of existence of a solution coincides with 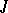 . For solutions of a non-linear system the maximal intervals of existence may differ for different solutions, and determining them is a difficult task. E.g. for the solution to the Cauchy problem
. For solutions of a non-linear system the maximal intervals of existence may differ for different solutions, and determining them is a difficult task. E.g. for the solution to the Cauchy problem
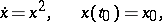 |
one has
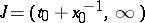 |
if 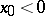 ,
,
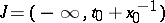 |
if 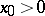 , and
, and
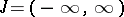 |
if  .
.
A sufficient condition under which one can indicate the maximal interval of existence of a solution is, e.g., Wintner's theorem: Suppose that the function 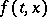 is continuous for
is continuous for 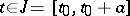 ,
,  , and that it satisfies in this domain the estimate
, and that it satisfies in this domain the estimate
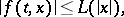 |
where 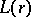 is a function continuous for
is a function continuous for 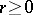 ,
, 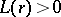 and for some
and for some 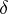 ,
, 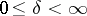 ,
,
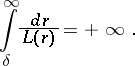 |
Then every solution of (2) exists on the whole of 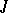 .
.
This theorem also holds for 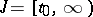 . Sufficient conditions for indefinite extendibility of a solution are of great interest. E.g., if
. Sufficient conditions for indefinite extendibility of a solution are of great interest. E.g., if  and its partial derivatives (3) are continuous for
and its partial derivatives (3) are continuous for 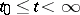 ,
,  , and if for these values of
, and if for these values of 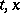 the estimates
the estimates
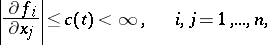 |
hold, then the solution of (2) with 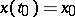 exists for
exists for 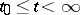 , for any
, for any 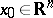 .
.
Consider the Cauchy problem
 | (4) |
for an autonomous system, where 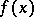 is continuously differentiable in a domain
is continuously differentiable in a domain 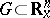 . If, as
. If, as  grows, the phase trajectory of the solution
grows, the phase trajectory of the solution 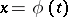 of (4) remains in a compact subset
of (4) remains in a compact subset 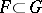 , then this solution can be extended to the semi-axis
, then this solution can be extended to the semi-axis 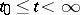 .
.
References
| [1] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
| [2] | V.I. Arnol'd, "Ordinary differential equations" , M.I.T. (1973) (Translated from Russian) |
| [3] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [4] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [5] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [6] | L. Cesari, "Asymptotic behavior and stability problems in ordinary differential equations" , Springer (1959) |
| [7] | A. Wintner, "The non-local existence problem of ordinary differential equations" Amer. J. Math. , 67 (1945) pp. 277–284 |
Comments
Instead of prolongation of solutions, continuation of solutions is nowadays mostly used.
Prolongation of solutions of differential equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Prolongation_of_solutions_of_differential_equations&oldid=48331