Projective algebraic set

A subset of points of a projective space defined over a field that has (in homogeneous coordinates) the form

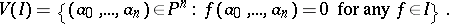Here is a homogeneous ideal in the polynomial ring . (An ideal is homogeneous if and , where the are homogeneous polynomials of degree 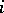, imply that .)

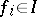Projective algebraic sets possess the following properties:

1) ;

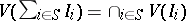2) ;

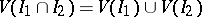3) if 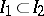, then ;

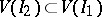4) 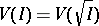, where 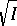is the radical of the ideal 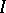(cf. Radical of an ideal).

It follows from properties 1)–3) that on 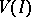the Zariski topology can be introduced. If 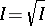, then can be uniquely represented as the intersection of homogeneous prime ideals:

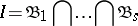and

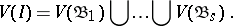In the case where 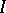is a homogeneous prime ideal, the projective algebraic set 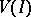is called a projective variety.

References

[1]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001
[2]	O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) MR0389876 MR0384768 Zbl 0313.13001

References

[a1]	D. Mumford, "Algebraic geometry" , 1. Complex projective varieties , Springer (1976) MR0453732 Zbl 0356.14002
[a2]	R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 MR0463157 Zbl 0367.14001