Preservation of domain, principle of

A property of holomorphic functions on domains in the complex plane: the set of values of every non-constant holomorphic function on a domain is also a domain, that is, an open connected set. The basic property here is that of openness of the image, which follows from Rouché's theorem or from the principle of the argument (cf. Rouché theorem; Argument, principle of the). The principle of preservation of domain can be considered as a generalization of the maximum-modulus principle for holomorphic functions.

The principle of preservation of domain holds for holomorphic functions on an arbitrary complex manifold: the set of values of any non-constant holomorphic function on a connected complex manifold is a domain in the complex plane. It also holds for holomorphic mappings from complex manifolds into Riemann surfaces. However, holomorphic mappings 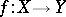into complex manifolds 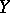of dimension exceeding 1 need not be open, in general: If 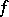is non-constant, but has rank everywhere less than 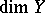, say, then the image 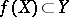has no interior points, in general. Openness can also be violated in the case when 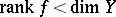on sets of small dimension. For example, under the mapping

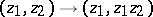from into itself, the image is the non-open set . The principle of preservation of domain holds for holomorphic mappings if the condition that be non-constant is replaced by stronger requirements, one of the simplest being the zero-dimensionality of the set of points for which .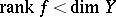

References

[1]	I.I. [I.I. Privalov] Priwalow, "Einführung in die Funktionentheorie" , 1–3 , Teubner (1965–1967) (Translated from Russian)
[2]	R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)

Comments

In the older German literature the concept occurs as the "GebietstreueGebietstreue" of a holomorphic mapping. In English, one usually speaks of the open mapping principle, cf. [a1].

References

[a1]	G.T. Whyburn, "Topological analysis" , Princeton Univ. Press (1964)
[a2]	E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian)