Pre-measure

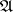A finitely-additive measure with real or complex values on some space having the property that it is defined on an algebra of subsets of of the form 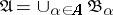, where 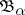is a family of 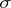-algebras of , labelled by the elements of some partially ordered set 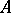, such that if 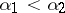, while the restriction of the measure to any 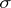-algebra is countably additive. 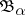E.g., if is a Hausdorff space, is the family of all compacta, ordered by inclusion, , , is the 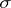-algebra of all Borel subsets of the compactum and is the space of all continuous functions on with compact support, then every linear functional on 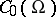that is continuous in the topology of uniform convergence in 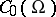generates a pre-measure on the algebra .

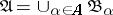Let be a locally convex linear space, let 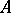be the set of finite-dimensional subspaces of the dual space 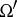, ordered by inclusion, and let , , 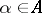be the least 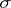-algebra relative to which all linear functionals are measurable. The sets of the algebra are called cylindrical sets, and any pre-measure on 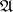is called a cylindrical measure (or quasi-measure). A positive-definite functional on 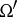that is continuous on any finite-dimensional subspace is the characteristic function (Fourier transform) of a finite non-negative pre-measure on .

References

[1]	N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French)

Comments

The term "pre-measure" is also used in the following, related but somewhat different, sense. Let 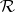be a ring of sets on some space , and a numerical function defined on 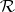. Then 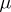is a pre-measure if

i) , 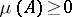for all ;

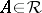ii) for every countable sequence of pairwise disjoint subsets 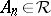such that .

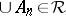If ii) only holds for finite disjoint sequences, 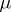is called a content. Not every content is a pre-measure.

References

[a1]	H. Bauer, "Probability theory and elements of measure theory" , Holt, Rinehart & Winston (1972) pp. 13ff (Translated from German)