Potential operator
From Encyclopedia of Mathematics
A mapping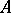 
of a Banach space 
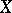into the dual space 
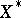that is the gradient of some functional 
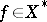, i.e. is such that
 |
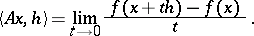For instance, any bounded self-adjoint operator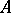 
defined on a Hilbert space 
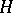is potential:
 |
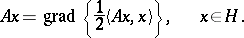References
| [1] | M.M. Vainberg, "Variational method and method of monotone operators in the theory of nonlinear equations" , Wiley (1973) (Translated from Russian) |
| [2] | H. Gajewski, K. Gröger, K. Zacharias, "Nichtlineare Operatorgleichungen und Operatordifferentialgleichungen" , Akademie Verlag (1974) |
How to Cite This Entry:
Potential operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_operator&oldid=48265
Potential operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_operator&oldid=48265
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article