Potential net
From Encyclopedia of Mathematics
Egorov net
An orthogonal net on a two-dimensional surface in Euclidean space that is mapped to itself by the potential motion of a fluid on this surface. In parameters of the potential net the line element of this surface has the form
 |
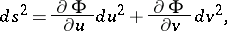where 
is the potential of the velocity field of the fluid. Each orthogonal semi-geodesic net is potential. A particular case of a potential net is a Liouville net. D.F. Egorov was the first (1901) to consider potential nets.
References
| [1] | D.F. Egorov, "Papers in differential geometry" , Moscow (1970) (In Russian) |
| [2] | V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian) |
How to Cite This Entry:
Potential net. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_net&oldid=48263
Potential net. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_net&oldid=48263
This article was adapted from an original article by V.T. Bazylev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article