Positive sequence
From Encyclopedia of Mathematics
A sequence 
of real numbers in the interval 
such that for any polynomial
 |
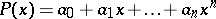that is not identically zero and is not negative on 
the expression
 |
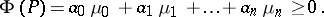If for any such polynomial 
, then the sequence is called strictly positive. For the sequence 
in 
to be positive, the existence of an increasing function 
on 
for which
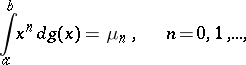 | (1) |
is necessary and sufficient.
Comments
A (strictly) negative sequence can be similarly defined and has a similar property. The problem of deciding whether for a given sequence 
of real numbers there is a positive Borel measure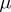 
on 
such that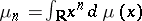 
is known as the Hamburger moment problem. The condition (1) is a moment condition, cf. Moment problem.
References
| [a1] | H.J. Landau (ed.) , Moments in mathematics , Amer. Math. Soc. (1987) pp. 56ff |
How to Cite This Entry:
Positive sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_sequence&oldid=48256
Positive sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_sequence&oldid=48256
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article