Positive functional

on an algebra 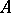with an involution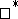

A linear functional 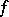on the 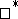-algebra 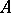that satisfies the condition 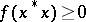for all 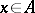. Positive functionals are important and have been introduced in particular because they are used in the GNS-construction, which is one of the basic methods for examining the structures of Banach 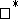-algebras. This and its generalizations, for example to weights in 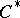-algebras, provide the basis for proving the theorem on the abstract characterization of uniformly-closed 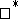-algebras of operators on a Hilbert space and the theorem on the completeness of a system of irreducible unitary representations of a locally compact group.

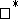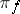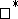The GNS-construction is a method for constructing a -representation of a -algebra 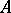with unit on a Hilbert space 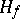for any positive functional 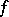on 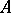, which is such that 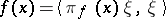for all 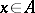, where 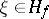is a certain cyclic vector. The construction is the following: The semi-inner product 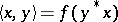is defined on 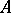; the corresponding neutral subspace is a left ideal 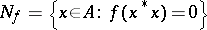, and therefore in the pre-Hilbert space 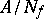left-multiplication operators 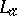by the elements 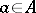(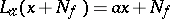) are well-defined; the operators 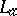are continuous and can be extended to continuous operators 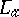on the completion 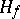of 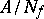. The mapping 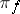that takes 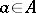to 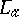is the required representation, where for 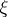one can take the image of the unit under the composition of the canonical mappings .

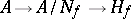References

[1]	I.M. Gel'fand, M.A. Naimark, "Normed involution rings and their representations" Izv. Akad. Nauk SSSR Ser. Mat. , 12 (1948) pp. 445–480 (In Russian)
[2]	I. Segal, "Irreducible representations of operator algebras" Bull. Amer. Math. Soc. , 53 (1947) pp. 73–88
[3]	M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)