Positive element

of an algebra 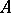with an involution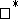

An element of of 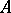the form 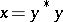, where 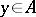. The set 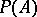of positive elements in a Banach -algebra 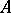contains the set 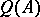of squares of the Hermitian elements, which in turn contains the set 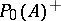of all Hermitian elements with positive spectrum (cf. Spectrum of an element), but in general it does not contain the set 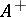of all Hermitian elements with non-negative spectrum. The condition 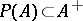defines the class of completely-symmetric (or Hermitian) Banach -algebras. For a -algebra to be completely symmetric it is necessary and sufficient that all Hermitian elements in it have real spectrum. The equality 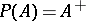holds if and only if 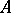is a 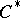-algebra. In that case 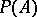is a reproducing cone (cf. Semi-ordered space) in the space of all Hermitian elements of the algebra .

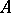References

[1]	M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)
[2]	J. Dixmier, "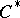 algebras" , North-Holland (1977) (Translated from French)
[3]	D.N. Raikov, Dokl. Akad. Nauk. SSSR , 54 : 5 (1946) pp. 391–394
[4]	V. Pták, "On the spectral radius in Banach algebras with involution" Bull. London Math. Soc. , 2 (1970) pp. 327–334
[5]	T.W. Palmer, "Hermitian Banach -algebras" Bull. Amer. Math. Soc. , 78 (1972) pp. 522–524