Pontryagin surface

A two-dimensional continuum , , 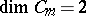in the four-dimensional Euclidean space 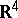such that its homological dimension modulo the given 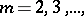is . In this sense these continua are "dimensionally deficient" . L.S. Pontryagin [1] has constructed surfaces 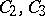such that their topological product 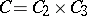is a continuum of dimension . Thus, the conjecture stating that under topological multiplication of two (metric) compacta their dimensions are added, was disproved. He proved this conjecture for homological dimensions modulo a prime number and, in general, over any group of coefficients which is a field. In [2] a two-dimensional continuum 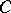in 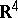has been constructed whose topological square 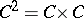is three-dimensional.

References

[1]	L.S. Pontryagin, "Sur une hypothèse fundamentale de la théorie de la dimension" C.R. Acad. Sci. Paris , 190 (1930) pp. 1105–1107
[2]	V.G. Boltyanskii, "On a theorem concerning addition of dimension" Uspekhi Mat. Nauk , 6 : 3 (1951) pp. 99–128 (In Russian)
[3]	P.S. Aleksandrov, "An introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian)

Comments

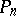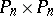
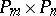
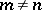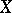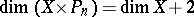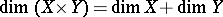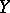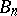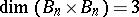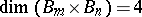In fact, Pontryagin constructed a sequence of surfaces , each of dimension 2, with -dimensional, but -dimensional if ; and these surfaces exhibit all possibilities in the sense that if a metric continuum satisfies for all , then for all metric continua . V.G. Boltyan'skii constructed -dimensional continua with the opposite behaviour, but for 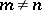; and these surfaces exhibit all possibilities, in the same sense.

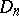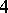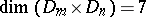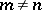Recently A.N. Dranishnikov showed that there even exist dimensionally-deficient absolute neighbourhood retracts (cf. e.g. Absolute retract for normal spaces; Retract of a topological space). His examples are -dimensional with for [a1].

References

[a1]	A.N. Dranishnikov, "Homological dimension theory" Russian Math. Surveys , 43 : 4 (1988) pp. 11–63 Uspekhi Mat. Nauk , 43 : 4 (1988) pp. 11–55